Trong lĩnh vực thống kê, sự phân bố của dữ liệu đóng vai trò quan trọng trong việc phân tích và hiểu rõ bản chất của hiện tượng. Để mô tả và đánh giá sự phân bố này, người ta thường sử dụng các đại lượng đặc trưng như phương sai và độ lệch chuẩn. Hai khái niệm này giúp xác định mức độ phân tán của các quan sát so với giá trị trung bình, cung cấp thông tin hữu ích về sự biến động và tính ổn định của dữ liệu. Bài viết này sẽ đi sâu vào giới thiệu và phân tích hai khái niệm quan trọng này, cùng với ứng dụng của chúng trong thống kê.
1. Phương sai là gì?
1.1. Định nghĩa phương sai
Phương sai là một đại lượng thống kê đo lường mức độ phân tán của các giá trị trong một tập dữ liệu so với giá trị trung bình của tập dữ liệu đó. Nói cách khác, phương sai là thước đo độ biến động của dữ liệu xung quanh trung bình.
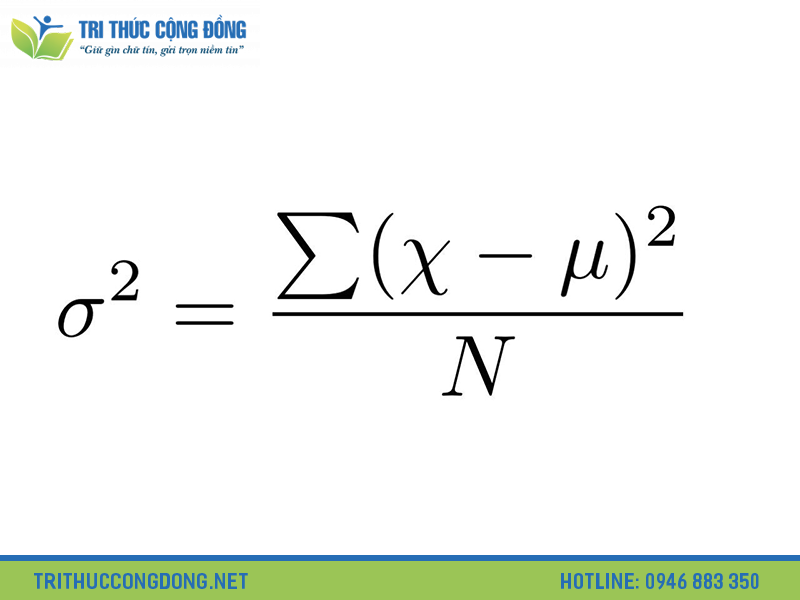
Phương sai là gì?
- Một phương sai lớn cho thấy các giá trị trong tập dữ liệu phân tán rộng so với trung bình, tức là có sự biến động lớn.
- Ngược lại, một phương sai nhỏ cho thấy dữ liệu tập trung gần giá trị trung bình, tức là có sự biến động thấp.
1.2. Công thức tính phương sai
Phương sai thường được ký hiệu là σ² và được tính toán theo công thức sau:
σ² = Σ (xi – x̄)² / n
Trong đó:
- n(population size): số lượng các giá trị trong tập dữ liệu
- xᵢ(data point): giá trị của một quan sát bất kỳ
- x̄(population mean): giá trị trung bình của tập dữ liệu
- σ²(population variance): phương sai tổng thể
Lưu ý:
- Công thức trên là công thức tính phương sai của mẫu dữ liệu.
- Trong thống kê, chúng ta thường sử dụng phương sai của mẫu để ước lượng phương sai của quần thể.
- Khi tính phương sai, chúng ta thường chia cho (n-1) thay vì n để có ước lượng không thiên vị về phương sai của quần thể.
>> Đọc thêm: Phương sai là gì? Công thức tính phương sai & ví dụ cụ thể
2. Độ lệch chuẩn là gì?
2.1. Định nghĩa độ lệch chuẩn
Độ lệch chuẩn là một đại lượng thống kê biểu thị mức độ phân tán của các giá trị trong một tập dữ liệu so với giá trị trung bình. Nói cách khác, độ lệch chuẩn là căn bậc hai của phương sai.
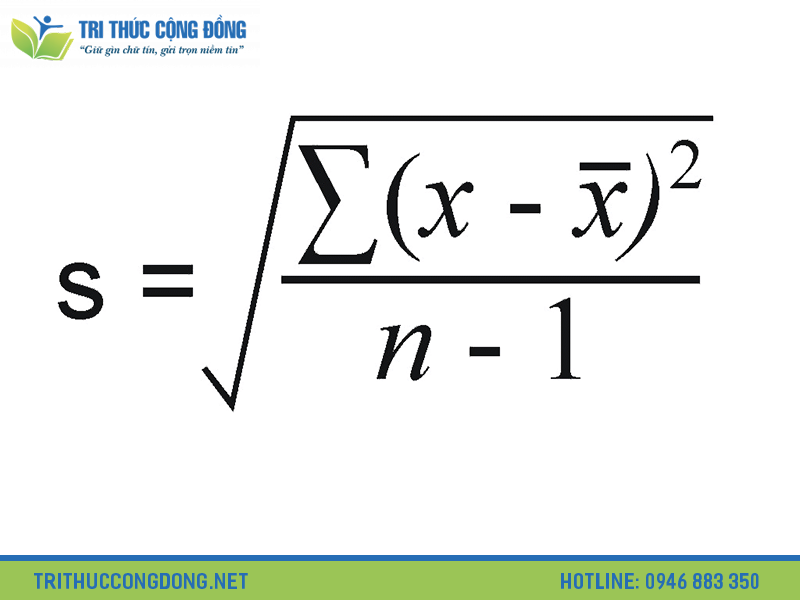
Độ lệch chuẩn là gì?
- Một độ lệch chuẩn lớn cho thấy các giá trị trong tập dữ liệu phân tán rộng so với trung bình, tức là dữ liệu có sự biến động lớn.
- Ngược lại, một độ lệch chuẩn nhỏ cho thấy dữ liệu tập trung gần giá trị trung bình, tức là dữ liệu ít biến động hơn.
2.2. Ý nghĩa của độ lệch chuẩn
Độ lệch chuẩn có ý nghĩa quan trọng trong thống kê vì nó cho phép chúng ta đánh giá mức độ biến động của dữ liệu:
- Phân tích dữ liệu: Độ lệch chuẩn cho phép chúng ta hiểu rõ hơn về sự phân tán của dữ liệu, giúp đưa ra những nhận xét và kết luận chính xác hơn về tập dữ liệu.
- So sánh dữ liệu: Độ lệch chuẩn cho phép chúng ta so sánh mức độ biến động của các tập dữ liệu khác nhau.
- Xây dựng mô hình: Độ lệch chuẩn được sử dụng trong việc xây dựng các mô hình thống kê như hồi quy tuyến tính, phân tích phương sai, v.v.
>> Tham khảo thêm: Dịch vụ viết thuê tiểu luận uy tín cho sinh viên các ngành
2.3. Công thức tính độ lệch chuẩn
Độ lệch chuẩn được tính bằng căn bậc hai của phương sai:
s = √σ²
Trong đó:
- s(sample standard deviation): độ lệch chuẩn mẫu
- σ²(population variance): phương sai
3. Ứng dụng của phương sai và độ lệch chuẩn trong thống kê
Phương sai và độ lệch chuẩn là những công cụ mạnh mẽ và được sử dụng rộng rãi trong nhiều lĩnh vực của thống kê, bao gồm:
3.1. Phân tích dữ liệu
- Xác định sự phân tán: Phương sai và độ lệch chuẩn giúp xác định mức độ phân tán của dữ liệu so với giá trị trung bình. Điều này giúp chúng ta hiểu rõ hơn về tính chất và sự biến động của dữ liệu.
- So sánh các nhóm dữ liệu: Phương sai và độ lệch chuẩn có thể được sử dụng để so sánh mức độ biến động của các nhóm dữ liệu khác nhau, chẳng hạn như so sánh hiệu quả của hai loại thuốc khác nhau.
- Kiểm tra giả thuyết: Phương sai và độ lệch chuẩn đóng vai trò quan trọng trong việc kiểm tra giả thuyết thống kê, chẳng hạn như kiểm tra xem liệu hai nhóm có phương sai bằng nhau hay không.
Ví dụ 1: Mô tả & so sánh độ biến động dữ liệu (Descriptive analytics)
Phân tích dữ liệu điểm kiểm tra của một lớp học và so sánh hai lớp/nhóm xem nhóm nào ổn định hơn.
Lớp A điểm: 6, 7, 7, 8, 12 → x̄ = 8; s ≈ 2.10
Lớp B điểm: 7, 7, 8, 8, 9 → x̄ ≈ 7,8; s ≈ 0,84
⇒ Lớp B ổn định hơn (độ lệch chuẩn nhỏ).
3.2. Xây dựng mô hình thống kê

Ứng dụng của phương sai và độ lệch chuẩn trong thống kê
- Hồi quy tuyến tính: Phương sai và độ lệch chuẩn được sử dụng để ước lượng sai số trong mô hình hồi quy tuyến tính, từ đó đánh giá độ chính xác của mô hình.
- Phân tích phương sai: Phương sai
củacác nhóm được sử dụng để kiểm tra sự khác biệt giữa các nhóm, chẳng hạn như so sánh hiệu quả của các phương pháp giảng dạy khác nhau.
Ví dụ: Cho bảng tần số ghép lớp : Tuổi thọ của bóng đèn (đơn vị: giờ). Hãy tính phương sai, độ lệch chuẩn.
| Tuổi thọ | Tần số |
| 1150 | 3 |
| 1160 | 6 |
| 1170 | 12 |
| 1180 | 6 |
| 1190 | 3 |
| Tổng | 30 |
Giải:
Trung bình cộng tuổi thọ của bóng đèn là:
x̄ = 1170
Tổng bình phương độ lệch khi tính phương sai là:
Dùng máy tính Casio fx-570VN PLUS, chuyển sang MODE 3 (STAT) → chọn 1-VAR rồi nhập dữ liệu theo cặp ta được:
σ² = Σ (xi - x̄)² = 3600
Vậy phương sai và độ lệch chuẩn của bóng đèn là:
σ² = 3600 : 30 = 120
σ = √120 ~ 10,95 giờ
Kết luận: Tuổi thọ trung bình của bóng đèn là 1170 giờ.
- Phương sai σ² = 120 cho biết mức độ phân tán của dữ liệu tuổi thọ quanh giá trị trung bình.
- Độ lệch chuẩn σ ≈ 10,95 (giờ) có nghĩa là tuổi thọ của các bóng đèn thường dao động khoảng ±11 giờ quanh mức trung bình 1170 giờ.
Như vậy, tuổi thọ bóng đèn khá ổn định, các giá trị không lệch nhiều so với trung bình, chứng tỏ chất lượng sản phẩm đồng đều.
3.3. Các lĩnh vực ứng dụng khác
- Nghiên cứu thị trường: Độ lệch chuẩn được sử dụng để đánh giá sự biến động của nhu cầu thị trường, giúp các doanh nghiệp đưa ra quyết định về sản xuất và tiếp thị sản phẩm.
- Quản lý tài chính: Phương sai và độ lệch chuẩn được sử dụng để đánh giá rủi ro của các đầu tư, hỗ trợ các nhà đầu tư đưa ra quyết định đầu tư hợp lý.
- Y tế công cộng: Độ lệch chuẩn được sử dụng để đánh giá sự biến động của tỷ lệ mắc bệnh, giúp các nhà dịch tễ học hiểu rõ hơn về sự lây lan của bệnh tật.
Ví dụ trong nghiên cứu thị trường khi áp dụng phương sai và độ lệch chuẩn:
Giả sử một công ty muốn nghiên cứu số lượng sản phẩm A bán ra mỗi tháng trong 6 tháng gần nhất:
Tháng 1: 480 sản phẩm
Tháng 2: 520 sản phẩm
Tháng 3: 600 sản phẩm
Tháng 4: 400 sản phẩm
Tháng 5: 500 sản phẩm
Tháng 6: 550 sản phẩm
Giải:
Trung bình cộng số lượng sản phẩm A bán ra mỗi tháng trong 6 tháng gần nhất là:
x̄ = 508,33
Tổng bình phương độ lệch khi tính phương sai là:
Dùng máy tính Casio fx-570VN PLUS, chuyển sang MODE 3 (STAT) → chọn 1-VAR rồi nhập dữ liệu theo cặp ta được:
σ² = Σ (xi - x̄)² = 23,894
Vậy phương sai và độ lệch chuẩn của số lượng sản phẩm A bán ra là:
σ² = 23 894,44 : 6 = 3982,41
σ = √3982,41 ~ 63,13
Kết luận:
- Trung bình số sản phẩm được bán ra trong 1 tháng là ~508 sản phẩm.
- Độ lệch chuẩn ~63 sản phẩm cho biết số lượng bán ra thường dao động khoảng ±63 sản phẩm so với mức trung bình.
- Như vậy, trong 6 tháng qua, doanh số sản phẩm A tương đối biến động, không đều đặn, có tháng cao hơn hoặc thấp hơn trung bình đến khoảng 60 sản phẩm.
Kết luận: Công ty có thể dự báo doanh số trung bình mỗi tháng ở mức ~500 sản phẩm, nhưng cần lưu ý sự dao động khoảng ±60 sản phẩm để chuẩn bị kế hoạch sản xuất và phân phối hợp lý.
Qua bài viết này, bạn đã hiểu rõ độ lệch chuẩn là gì và mối quan hệ của nó với phương sai trong thống kê. Cả hai đại lượng này đều giúp mô tả sự phân bố dữ liệu, đánh giá mức độ biến động và tính ổn định của hiện tượng nghiên cứu. Với ứng dụng rộng rãi trong phân tích dữ liệu, mô hình hóa, tài chính và nghiên cứu khoa học, phương sai và độ lệch chuẩn được xem là nền tảng của mọi phân tích thống kê chính xác và khách quan.
Hy vọng những chia sẻ của Tri Thức Cộng Đồng về phương sai và độ lệch chuẩn sẽ giúp bạn đạt điểm cao trong quá trình học tập. Bên cạnh đó, nếu bạn cần hỗ trợ về dịch vụ chạy SPSS thuê, vui lòng liên hệ ngay với chúng tôi để được tư vấn chi tiết hơn nhé!
Thông tin liên hệ:
- Hotline: 094 688 3350
- Website: https://trithuccongdong.net/
- Email: ttcd.group@gmail.com
- Địa chỉ:
144 Xuân Thủy, Dịch Vọng Hậu, Cầu Giấy, Hà Nội
2 Võ Oanh, Phường 25, Bình Thạnh, Hồ Chí Minh
9 Đại lộ Temasek, Suntec Tower, Singapore

 14 Tháng 1, 2026
14 Tháng 1, 2026 Share
Share