Phương Sai Là Gì? Cách Tính Và Ý Nghĩa Trong Đầu Tư Tài Chính

Trong thống kê, việc hiểu rõ dữ liệu phân tán như thế nào quanh giá trị trung bình là yếu tố then chốt để phân tích chính xác. Vậy phương sai là gì mà lại được xem là thước đo quan trọng phản ánh mức độ biến động của các con số? Khái niệm này không chỉ xuất hiện trong sách giáo khoa mà còn đóng vai trò lớn trong nghiên cứu, phân tích dữ liệu và tài chính – đầu tư. Hãy cùng Tri Thức Cộng Đồng tìm hiểu qua bài viết dưới đây.

1. Phương sai là gì?

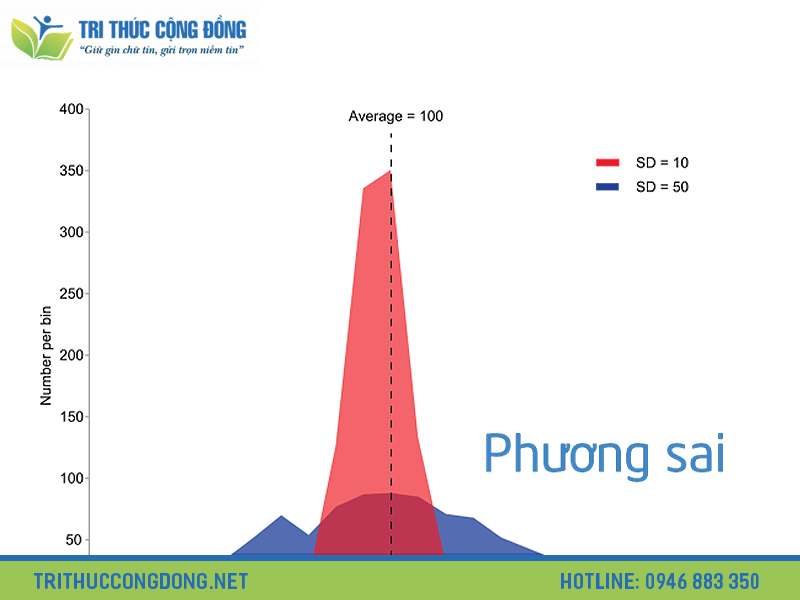
Phương sai (Variance) là phép đo mức chênh lệch giữa các số liệu trong một tập dữ liệu trong thống kê. Nó đo khoảng cách giữa mỗi số liệu với nhau và với giá trị trung bình của tập dữ liệu.

Phương sai được ký hiệu là σ². Trong thống kê, đây là một trong những tham số cơ bản phản ánh mức độ phân tán của dữ liệu. Trong đầu tư tài chính, phương sai lợi nhuận của các tài sản trong danh mục đầu tư được sử dụng để đánh giá và so sánh hiệu quả giữa các tài sản cũng như với giá trị trung bình của danh mục.

Phương sai (Variance) là gì?

2. Công thức tính phương sai

Phương sai được tính bằng cách xác định giá trị chênh lệch giữa mỗi số trong tập dữ liệu với giá trị trung bình, sau đó bình phương các chênh lệch và chia tổng đó cho số lượng quan sát trong tập dữ liệu.

Công thức tổng quát:

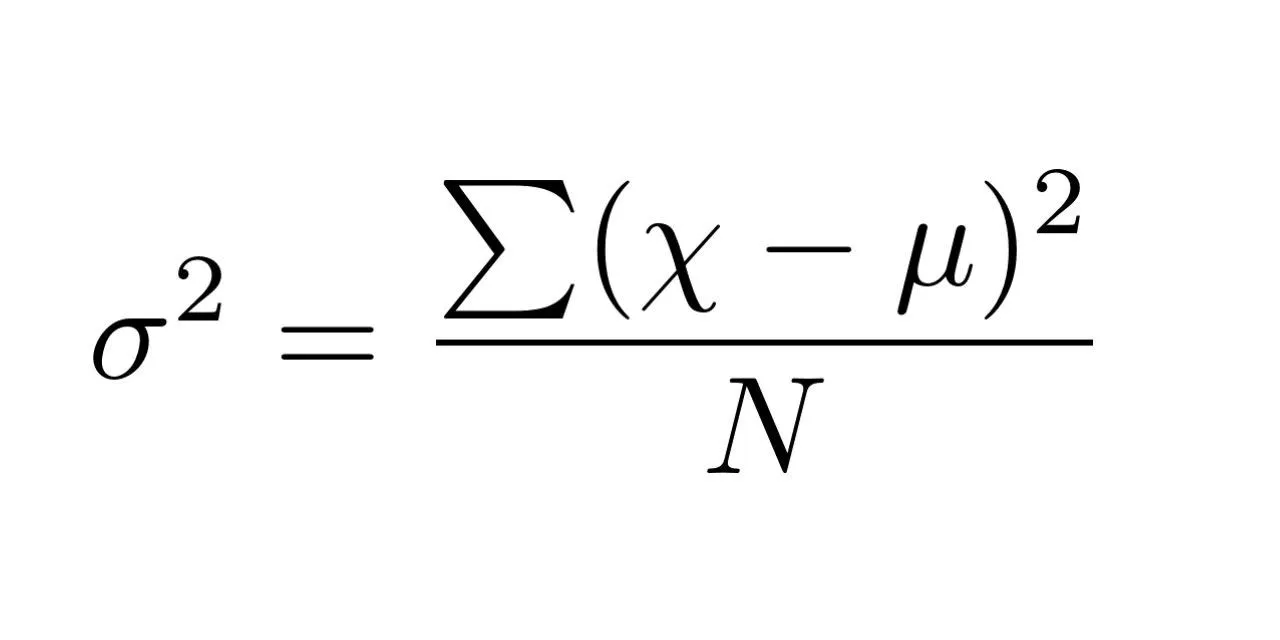
Công thức tổng quát tính phương sai

Trong đó:

• Xi: giá trị quan sát thứ i
• μ: giá trị trung bình của tập dữ liệu
• N: tổng số lượng quan sát

Khi tính phương sai mẫu để ước lượng phương sai tổng thể, mẫu số của công thức được thay bằng N−1 để bảo đảm ước lượng không thiên vị và không đánh giá thấp phương sai tổng thể.

>> Đọc thêm: Quản lý Giáo dục tiểu học là gì? Các kỹ năng cần có

3. Cách tính phương sai

Để tính phương sai, thực hiện theo các bước sau:

• Bước 1: Tính giá trị trung bình của tập dữ liệu.
• Bước 2:Tính chênh lệch giữa từng giá trị và giá trị trung bình.
• Bước 3:Bình phương từng chênh lệch để loại bỏ dấu âm.
• Bước 4:Cộng tất cả các bình phương sai lệch lại.
• Bước 5:Chia tổng đó cho N (với tổng thể) hoặc N−1 (với mẫu).

Phương sai cho thấy mức độ các giá trị dữ liệu nằm xa giá trị trung bình đến đâu: phương sai càng lớn, dữ liệu càng phân tán; phương sai càng nhỏ, dữ liệu càng tập trung quanh trung bình.

Ví dụ: Giả sử lợi nhuận của một cổ phiếu trong ba năm lần lượt là 10%, 20% và -15%.

• Giá trị trung bình là:  (10 + 20 – 15) / 3 = 5%
• Chênh lệch so với trung bình lần lượt là: 5%, 15%, – 20%.
• Bình phương các sai lệch: 25%, 225%, 400%.
• Tổng các bình phương sai lệch là 650%.
• Chia cho số quan sát (3) ta được phương sai là 216,67%.
• Nếu chia cho N−1 (2), ta được phương sai mẫu là 3,25% (0,0325).
• Độ lệch chuẩn là căn bậc hai của phương sai, bằng khoảng 14,72% hoặc 18% tùy theo cách tính.

4. Ưu điểm và nhược điểm của phương sai

Ưu điểm

• Là thước đo đơn giản và trực quan để xem các giá trị dữ liệu phân tán như thế nào.
• Xem tất cả các sai lệch so với trung bình là như nhau, bất kể hướng tăng hay giảm.
• Tránh được tình trạng các sai lệch triệt tiêu lẫn nhau, giúp thể hiện đúng mức biến động của dữ liệu.

Nhược điểm

• Bình phương các sai lệch khiến phương sai nhạy cảm với các giá trị ngoại lai, có thể làm lệch kết quả.
• Đơn vị của phương sai là bình phương của đơn vị dữ liệu ban đầu, gây khó khăn trong việc diễn giải trực tiếp.
• Thường được dùng như bước trung gian để tính độ lệch chuẩn – chỉ số dễ hiểu hơn.

>> Tham khảo thêm: Dịch vụ viết thuê tiểu luận uy tín, đảm bảo tiến độ nộp bài

5. Ứng dụng của phương sai

5.1. Thống kê học và phân tích dữ liệu

• Phân tích dữ liệu thăm dò: Phương sai giúp xác định các giá trị cực đoan, ngoại lệ hoặc bất thường trong tập dữ liệu.
• Kiểm định giả thuyết: Phương sai được sử dụng trong các kiểm định thống kê để đánh giá sự khác biệt giữa các nhóm dữ liệu.
• Dự đoán: Phương sai được sử dụng để đo độ chính xác của các mô hình dự đoán.

Phương sai đo lường sự khác biệt giữa các giá trị dữ liệu so với trung bình, giúp xác định mức độ phân tán của tập dữ liệu.

5.2. Kiểm soát chất lượng sản phẩm

• Phương sai được sử dụng trong kiểm soát chất lượng để theo dõi độ biến động của các đặc tính sản phẩm và xác định các lỗi tiềm ẩn trong quá trình sản xuất.
• Ví dụ, một công ty sản xuất bóng đèn có thể sử dụng phương sai tuổi thọ bóng đèn để giám sát sự nhất quán của sản phẩm.

5.3. Đánh giá rủi ro trong đầu tư tài chính

• Phương sai được sử dụng trong đánh giá rủi ro để đo lường mức độ biến động của giá chứng khoán, trái phiếu hoặc các công cụ tài chính khác.
• Độ biến động cao hơn (phương sai lớn hơn) cho biết rủi ro đầu tư cao hơn.

Phương sai là công cụ quan trọng giúp chúng ta hiểu rõ hơn về mức độ biến động của dữ liệu hoặc lợi nhuận đầu tư quanh giá trị trung bình. Một phương sai lớn thể hiện dữ liệu có sự chênh lệch cao và biến động mạnh, trong khi phương sai nhỏ cho thấy sự ổn định và tập trung. Dù việc diễn giải phương sai đôi khi khó khăn do đơn vị tính là bình phương, nhưng nó vẫn đóng vai trò nền tảng cho các phép đo thống kê khác như độ lệch chuẩn chỉ số phổ biến hơn trong việc đánh giá rủi ro và sự biến động trong thực tiễn. Việc hiểu rõ độ lệch chuẩn là gì, công thức và cách áp dụng không chỉ giúp học tốt môn toán mà còn mang lại nhiều giá trị thực tiễn trong nghiên cứu và công việc.