Trong quá trình phân tích dữ liệu, chúng ta không chỉ quan tâm đến giá trị trung bình mà còn muốn hiểu dữ liệu đó phân tán hay ổn định đến mức nào. Chính vì vậy, khái niệm độ lệch chuẩn là gì trở thành một yếu tố then chốt trong thống kê mô tả.
Độ lệch chuẩn giúp đo lường mức độ chênh lệch giữa các giá trị trong tập dữ liệu so với giá trị trung bình, từ đó phản ánh mức độ biến động và tính ổn định của hiện tượng được nghiên cứu. Nhờ vậy, nó được ứng dụng rộng rãi trong nhiều lĩnh vực như kinh tế, tài chính, giáo dục hay nghiên cứu khoa học, giúp người phân tích có cái nhìn toàn diện và chính xác hơn về dữ liệu.

Khái niệm độ lệch chuẩn
1. Độ lệch chuẩn là gì?
Độ lệch chuẩn (Standard Deviation) là một đại lượng thống kê dùng để phản ánh mức độ phân tán của các giá trị trong một bộ dữ liệu so với giá trị trung bình của chúng. Đây là một thước đo quan trọng trong thống kê mô tả, thể hiện mức độ biến thiên của dữ liệu trong một thời điểm và phản ánh xu thế của sự thay đổi.
- Nếu hai tập dữ liệu có cùng giá trị trung bình, thì tập nào có độ lệch chuẩn lớn hơn chính là tập có độ biến động cao hơn.
- Ngược lại, nếu hai tập dữ liệu có trung bình khác nhau, việc so sánh độ lệch chuẩn của chúng không còn ý nghĩa thống kê.
Trong thực tế, độ lệch chuẩn giúp các nhà kinh tế, nhà quản lý hay nhà nghiên cứu quan sát, dự báo và đánh giá mức độ ổn định hoặc biến động của hiện tượng trong nhiều lĩnh vực khác nhau như kinh tế, giáo dục, xã hội hay kỹ thuật.
>> Đọc thêm: Du học thạc sĩ Đài Loan & những điều cần biết
2. Công thức tính độ lệch chuẩn
Độ lệch chuẩn mẫu(Sample Standard Deviation) được xác định thông qua công thức:
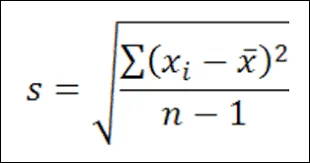
Công thức tính độ lệch chuẩn
Trong đó:
- S: Độ lệch chuẩn mẫu
- σ: Độ lệch chuẩn tổng thể
- xᵢ: Giá trị quan sát thứ i
- x̄: Giá trị trung bình của các quan sát
- n hoặc N: Số phần tử trong mẫu hoặc tổng thể
Độ lệch chuẩn chính là căn bậc hai của phương sai, và cả hai đại lượng này đều dùng để đo lường mức độ lan truyền của dữ liệu quanh giá trị trung bình.
>> Tham khảo thêm: Nhận viết tiểu luận thuê uy tín cho sinh viên đại học
3. Các bước tính độ lệch chuẩn
3.1. Bước 1: Tính giá trị trung bình
Cộng tất cả các giá trị trong bộ dữ liệu và chia cho tổng số phần tử.
Ví dụ: Với dãy số 10, 8, 10, 8, 8, 4
→ Tổng = 48, số lượng = 6
→ Trung bình = 48 / 6 = 8
3.2. Bước 2: Tính phương sai
- Lấy từng giá trị trừ đi giá trị trung bình để tìm khoảng cách.
- Bình phương các khoảng cách này.
- Cộng tất cả giá trị bình phương.
- Chia cho (n – 1) nếu là mẫu, hoặc N nếu là tổng thể.
Ví dụ:
Khoảng cách n-1 : 2, 0, 2, 0, 0, -4
Bình phương các giá trị: 4, 0, 4, 0, 0, 16
Tổng bình phương = 24
Phương sai = 24 / (6−1) = 4,8
3.3. Bước 3: Tính độ lệch chuẩn
Độ lệch chuẩn là căn bậc hai của phương sai.
SD = √4,8 = 2,19
Kết quả: Độ lệch chuẩn = 2,19
4. Cách tính độ lệch chuẩn trong Excel và SPSS
4.1. Tính độ lệch chuẩn trong Excel
Trong Excel, bạn có thể sử dụng các hàm sau:
- Độ lệch chuẩn của mẫu:
=STDEV.S(number1, [number2], …) - Độ lệch chuẩn của toàn bộ quần thể:
=STDEV.P(number1, [number2], …)
Cách dùng:
- Nhập các giá trị (hoặc vùng dữ liệu) vào hàm.
- Excel sẽ tự động tính độ lệch chuẩn dựa trên hàm bạn chọn.
Ví dụ:
Cho bảng điểm của 10 học sinh dưới đây:
| Học sinh | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Điểm | 6.5 | 7 | 8.2 | 5 | 5.5 | 9.0 | 6.8 | 7.2 | 8.5 | 6.0 |
- Tính độ lệch chuẩn của mẫu (sample standard deviation) cho tập dữ liệu trên.
- Tính độ lệch chuẩn của quần thể (population standard deviation) cho cùng dữ liệu.
Giải:
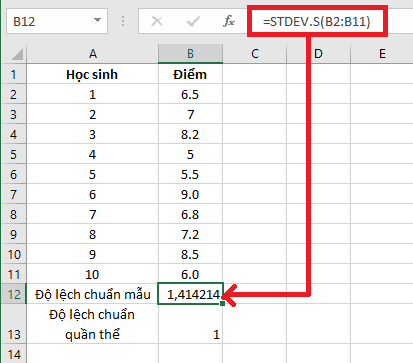
Cách tính độ lệch chuẩn trong Excel
Vậy độ lệch chuẩn của mẫu (sample standard deviation) là 1,414. Còn độ lệch chuẩn quần thể bằng 1
4.2. Tính độ lệch chuẩn trong SPSS
Trong phần thống kê mô tả, độ lệch chuẩn biểu thị mức độ khác biệt giữa các câu trả lời của đáp viên.
Bước 1: Nhập dữ liệu vào SPSS
Bước 2: Chọn thống kê mô tả: Analyze → Descriptive Statistics → Descriptives
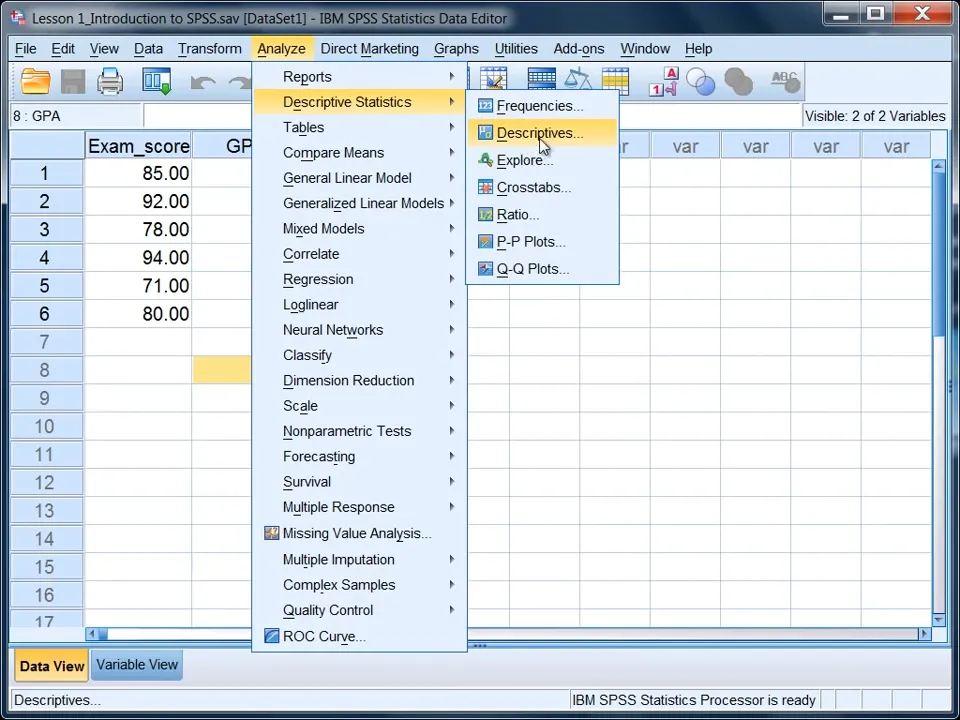
Cách tính độ lệch chuẩn trong SPSS
Bước 3: Chọn biến cần tính rồi sang Variables
Bước 4: Chọn thông số cần tính ở phần Options. Ticks Mean (Trung bình), Std. deviation (Độ lệch chuẩn),… rồi Continue.
Bước 5: Chọn OK rồi đợi Kết quả
- Độ lệch chuẩn thấp → Các câu trả lời gần giống nhau.
- Độ lệch chuẩn cao → Câu trả lời phân tán, không đồng nhất.
SPSS không quy định một mức “tốt” hay “xấu” cho độ lệch chuẩn. Giá trị này chỉ giúp xác định dữ liệu có tập trung như kỳ vọng nghiên cứu hay không.
5. Ý nghĩa của độ lệch chuẩn
Độ lệch chuẩn cho biết mức độ biến động của dữ liệu so với trung bình.
- Khi độ lệch chuẩn thấp, dữ liệu gần nhau → tính ổn định cao.
- Khi độ lệch chuẩn cao, dữ liệu phân tán → tính biến động lớn.
Trong lĩnh vực đầu tư và giao dịch tài chính, độ lệch chuẩn là công cụ đo rủi ro thị trường.
- Khi giá thay đổi mạnh so với trung bình → độ lệch chuẩn cao → thị trường biến động mạnh.
- Khi giá ổn định → độ lệch chuẩn thấp → thị trường bình ổn.
Nhờ độ lệch chuẩn, nhà đầu tư có thể dự đoán thời điểm đảo chiều xu thế, xác định vùng đỉnh hoặc đáy, và tận dụng cơ hội thị trường trong giai đoạn biến động.

Ý nghĩa của độ lệch chuẩn
6. Ví dụ minh họa
6.1. Phân tích điểm thi môn Toán của học sinh
Giả sử bạn có dữ liệu điểm thi môn Toán của một lớp học: 5, 6, 7, 8, 9, 9, 10, 11, 12, 13
- Tính trung bình: (5 + 6 + 7 + 8 + 9 + 9 + 10 + 11 + 12 + 13) / 10 = 9
- Tính phương sai: [(5 – 9)² + (6 – 9)² + (7 – 9)² + (8 – 9)² + (9 – 9)² + (9 – 9)² + (10 – 9)² + (11 – 9)² + (12 – 9)² + (13 – 9)²] / 9 = 2,67
- Tính độ lệch chuẩn: √2,67 = 1,63
Độ lệch chuẩn là 1,63 cho biết các điểm thi phân tán quanh trung bình là 9 với khoảng cách xấp xỉ 1,63 điểm.
6.2. Đánh giá hiệu quả của chiến dịch marketing
Giả sử một chiến dịch marketing thu thập dữ liệu về doanh thu bán hàng: 1000, 1100, 1200, 1300, 1400, 1400, 1500, 1600, 1700, 1800
- Tính trung bình: (1000 + 1100 + 1200 + 1300 + 1400 + 1400 + 1500 + 1600 + 1700 + 1800) / 10 = 1400
- Tính phương sai: [(1000 – 1400)² + (1100 – 1400)² + (1200 – 1400)² + (1300 – 1400)² + (1400 – 1400)² + (1400 – 1400)² + (1500 – 1400)² + (1600 – 1400)² + (1700 – 1400)² + (1800 – 1400)²] / 9 = 64000
- Tính độ lệch chuẩn: √64000 = 253
Độ lệch chuẩn là 253 cho biết doanh thu bán hàng phân tán quanh trung bình là 1400 với khoảng cách xấp xỉ 253 đô la.
Ngoài ra, bạn có thể sử dụng phần mềm SPSS để phân tích dữ liệu phổ biến cung cấp nhiều công cụ để tính toán và phân tích độ lệch chuẩn.

Đánh giá hiệu quả của chiến dịch marketing
Độ lệch chuẩn là thước đo đặc trưng cho độ biến thiên của dữ liệu, cho thấy các giá trị trong một tập hợp phân tán nhiều hay ít quanh giá trị trung bình. Một độ lệch chuẩn thấp biểu thị sự ổn định và đồng nhất, trong khi độ lệch chuẩn cao phản ánh sự biến động mạnh. Với khả năng mô tả mức độ rủi ro, dao động và xu thế của dữ liệu, độ lệch chuẩn đóng vai trò cốt lõi trong phân tích thống kê, là nền tảng quan trọng giúp nhà nghiên cứu và nhà quản lý hiểu sâu hơn về bản chất của dữ liệu và ra quyết định chính xác hơn.

 14 Tháng 1, 2026
14 Tháng 1, 2026 Share
Share