Hồi quy tuyến tính là một trong những mô hình thống kê cơ bản và phổ biến nhất trong phân tích dữ liệu. Phương pháp này giúp xác định mối quan hệ giữa các biến và dự đoán kết quả dựa trên dữ liệu có sẵn. Bài viết dưới đây sẽ giúp bạn hiểu rõ hồi quy tuyến tính là gì, cách hoạt động, các loại hồi quy phổ biến và ứng dụng thực tế của mô hình này.
1. Hồi quy tuyến tính là gì?
Hồi quy tuyến tính (Linear Regression) là một phương pháp thống kê nhằm mô tả mối quan hệ tuyến tính giữa biến phụ thuộc (Y) và một hoặc nhiều biến độc lập (X).
- Hồi quy tuyến tính đơn: chỉ có một biến độc lập.
- Hồi quy tuyến tính đa biến: có từ hai biến độc lập trở lên.

Hồi quy tuyến tính là gì ?
2. Tại sao hồi quy tuyến tính lại quan trọng?
Các mô hình hồi quy tuyến tính có cấu trúc tương đối đơn giản, đồng thời mang lại một biểu thức toán học rõ ràng và dễ hiểu giúp dự đoán các giá trị chưa biết. Đây là một trong những phương pháp thống kê được sử dụng rộng rãi và lâu đời nhất, nhờ khả năng triển khai linh hoạt trên nhiều phần mềm và nền tảng tính toán khác nhau.
Trong thực tiễn, doanh nghiệp ứng dụng hồi quy tuyến tính để biến đổi dữ liệu thô thành thông tin có giá trị, phục vụ cho việc ra quyết định kinh doanh, dự báo xu hướng thị trường và tối ưu hóa chiến lược. Giới khoa học trong các lĩnh vực như sinh học, tâm lý học, kinh tế, xã hội học và môi trường học cũng thường xuyên sử dụng phương pháp này để phân tích mối quan hệ giữa các biến và dự đoán xu hướng tương lai.
Bên cạnh đó, trong khoa học dữ liệu và trí tuệ nhân tạo, hồi quy tuyến tính được xem là nền tảng của nhiều thuật toán học máy hiện đại, giúp mô hình hóa dữ liệu, tìm ra quy luật tiềm ẩn và giải quyết các bài toán dự đoán phức tạp với độ chính xác cao.
3. Hồi quy tuyến tính hoạt động như thế nào?
3.1. Công thức tính hồi quy tuyến tính đơn
Hồi quy tuyến tính là một mô hình dùng để tìm cách biểu diễn mối quan hệ giữa hai tập dữ liệu – một biến độc lập (X) và một biến phụ thuộc (Y) để thể hiện xu hướng của dữ liệu.
Mục tiêu của mô hình này là tìm phương trình tuyến tính có dạng:
Y = aX + b
Trong đó:
- Biến độc lập (X) được đặt trên trục hoành (trục X) và đóng vai trò là yếu tố dự báo hoặc nguyên nhân.
- Biến phụ thuộc (Y) được đặt trên trục tung (trục Y) và thể hiện kết quả hoặc phản hồi từ biến X.
- a là hệ số góc (cho biết mức độ thay đổi của Y khi X tăng 1 đơn vị),
- b là hằng số chặn (giá trị của Y khi X = 0).
3.2. Quy trình hoạt động của hồi quy tuyến tính
- Bước 1: Thu thập dữ liệu gồm các cặp giá trị (X, Y). Ví dụ: (1, 5), (2, 8), (3, 11).
- Bước 2: Biểu diễn dữ liệu trên đồ thị bằng các điểm trên hệ trục tọa độ để quan sát xu hướng.
- Bước 3: Xác định đường thẳng phù hợp nhất (best fit line) bằng phương pháp bình phương tối thiểu (OLS). Mô hình sẽ tìm đường thẳng sao cho khoảng cách giữa các điểm dữ liệu và đường thẳng là nhỏ nhất có thể. Khoảng cách này gọi là phần dư (residual).
- Bước 4: Tính toán các hệ số hồi quy (a và b) thông qua công thức toán học hoặc phần mềm thống kê, mô hình xác định hệ số góc và hằng số chặn.
- Bước 5: Sử dụng mô hình để dự đoán giá trị Y cho bất kỳ giá trị X nào. Ví dụ: khi X = 4 → Y = 3×4 + 2 = 14.
4. Phương trình hồi quy tuyến tính
4.1. Hồi quy tuyến tính đơn (mô hình quần thể)
Mô hình hồi quy tuyến tính đơn ở mức quần thể (population regression model) được viết dưới dạng:
Y = β0 + β1X + ε
- Y: Biến phụ thuộc (Dependent Variable), giá trị của Y phụ thuộc vào X. Là hiện tượng, kết quả bạn muốn giải thích
- X: Biến độc lập (Independent Variable)
- β0: Hằng số chặn (Intercept) cho biết điểm xuất phát của đường hồi quy.
- β1: Hệ số góc (Slope). Cho biết Y thay đổi bao nhiêu khi X tăng 1 đơn vị.
- ε: Sai số ngẫu nhiên (Error term). Đại diện cho tất cả yếu tố khác ảnh hưởng đến Y mà mô hình không đo được.
Hồi quy tuyến tính đơn giúp phân tích mối quan hệ giữa hai yếu tố, ví dụ:
- Lượng mưa ảnh hưởng đến sản lượng nông nghiệp,
- Tuổi tác liên quan đến chiều cao của trẻ em,
- Nhiệt độ và sự giãn nở của kim loại trong thí nghiệm vật lý.
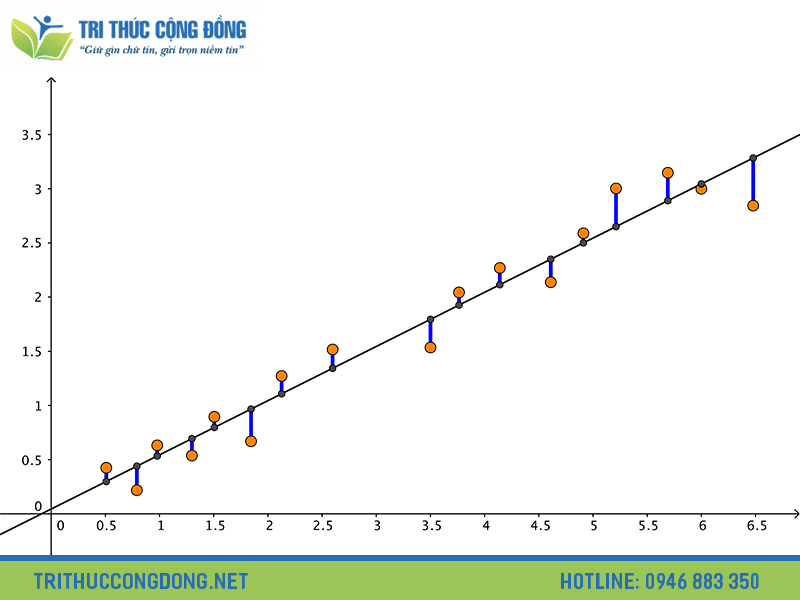
Phương trình hồi quy tuyến tính
4.2. Hồi quy tuyến tính đơn (ước lượng từ mẫu)
Trong thực tế, chúng ta không bao giờ biết chính xác hệ số thật của quần thể (β₀, β₁). Vì vậy, khi làm phân tích hồi quy, ta phải ước lượng các hệ số đó từ dữ liệu mẫu thu thập được.
Phương trình hồi quy mẫu được viết là:
Ŷ = β̂0 + β̂1X
Trong đó:
- Ŷ: giá trị Y dựa trên mô hình dự đoán
- β̂₀(intercept): ước lượng của hằng số chặn β₀
- β̂₁(slope): ước lượng của hệ số góc β₁
Các giá trị này được tính bằng phương pháp bình phương tối thiểu (OLS), sao cho tổng bình phương phần dư nhỏ nhất
4.3. Công thức ước lượng OLS (Hồi quy tuyến tính đơn)
Với mô hình:
Ŷ = β̂0 + β̂1X
Ta ước lượng các hệ số bằng phương pháp bình phương tối thiểu (OLS):
β̂1 = Σ(xi − x̄)(yi − ȳ) / Σ(xi − x̄)2
β̂0 = ȳ − β̂1x̄
Công thức này được dùng khi chỉ có một biến độc lập X. Với mục tiêu tìm đường thẳng có tổng bình phương phần dư nhỏ nhất.
4.4. Hồi quy tuyến tính đa biến (hay hồi quy tuyến tính bội)
Khi có nhiều biến độc lập, mô hình mở rộng thành:
Y = β0 + β1X1 + β2X2 + … + βpXp + ε
Trong đó:
- Y: biến phụ thuộc
- X₁ → Xp: các biến độc lập
- β₀, β₁, …, βp: hệ số hồi quy của quần thể
- ε: sai số ngẫu nhiên
Mỗi hệ số β thể hiện mức độ ảnh hưởng của từng biến độc lập lên kết quả Y. Ví dụ:
- Sản lượng cây trồng phụ thuộc vào lượng mưa, nhiệt độ và lượng phân bón,
- Rủi ro bệnh tim chịu tác động của chế độ ăn uống và tần suất tập thể dục,
- Lãi suất vay cá nhân bị ảnh hưởng bởi tăng trưởng thu nhập và tỷ lệ lạm phát.
4.5. Dạng ma trận tổng quát (General Linear Model)
Hồi quy tuyến tính bội có thể viết gọn bằng ký hiệu ma trận:
y = Xβ + ε
Trong đó:
- y: vector n×1 giá trị của biến phụ thuộc
- X: ma trận dữ liệu (n×(p+1)), cột đầu toàn số 1(intercept) và các biến X
- β: vector hệ số hồi quy (p+1)×1
- ε: vector sai số n x 1
4.6. Nghiệm OLS tổng quát
Hệ số hồi quy ước lượng (β̂) được tính bằng công thức:
β̂ = (XᵀX)⁻¹Xᵀy
Công thức trên là nghiệm tìm tập β̂ sao cho tổng bình phương phần dư nhỏ nhất được áp dụng cho cả hồi quy đơn và hồi quy bội.
5. Hồi quy tuyến tính trong máy học là gì
Trong máy học, hồi quy tuyến tính (Linear Regression) được xem là một thuật toán dự đoán có giám sát (supervised prediction algorithm), nơi máy tính học mối quan hệ giữa biến đầu vào (X) và đầu ra (Y) từ dữ liệu có sẵn.
Khác với thống kê truyền thống vốn nhấn mạnh vào ước lượng, kiểm định giả thuyết và ý nghĩa thống kê, hồi quy tuyến tính trong máy học tập trung vào khả năng dự đoán giá trị mới. Đây là bước nền tảng trong khoa học dữ liệu.
5.1. Mối quan hệ tuyến tính
Để mô hình hoạt động chính xác, mối quan hệ giữa X và Y phải gần tuyến tính. Điều này có nghĩa là khi X tăng (hoặc giảm), Y cũng thay đổi theo một xu hướng tương đối đều đặn.
Các nhà khoa học dữ liệu thường vẽ biểu đồ phân tán (scatter plot) để kiểm tra điều này. Nếu dữ liệu không tuyến tính, có thể biến đổi toán học như logarit hoặc căn bậc hai để tạo mối quan hệ tuyến tính hơn.
5.2. Phần dư độc lập (Independence of Residuals)
Trong hồi quy tuyến tính, phần dư (residual) là khoảng chênh lệch giữa giá trị thực tế và giá trị mà mô hình dự đoán. Để mô hình hoạt động đúng và không bị sai lệch, các phần dư cần độc lập với nhau — tức là chúng phải phân bố ngẫu nhiên, không có xu hướng hay quy luật theo thời gian hoặc theo bất kỳ trật tự nào.
Nếu phần dư tăng dần theo thời gian, mô hình chưa chuẩn. Kiểm định Durbin–Watson thường được dùng để phát hiện sự phụ thuộc trong phần dư.
5.3. Phần dư có phân phối chuẩn
Một mô hình hồi quy tốt có phần dư (residuals) phân bố chuẩn quanh giá trị trung bình bằng 0 theo dạng gần chuẩn (normal distribution). Biểu đồ Q–Q (Quantile–Quantile plot) giúp kiểm tra giả định này.
Nếu phần dư lệch chuẩn do ngoại lai hoặc dữ liệu bất thường, ta có thể loại bỏ hoặc biến đổi dữ liệu để cải thiện độ chính xác của mô hình.
5.4. Phương sai không đổi (Homoscedasticity)
Giả định cuối cùng là phương sai của phần dư phải không đổi với mọi giá trị X. Điều này nghĩa là sai số của mô hình cần phân bố đều, không tăng hoặc giảm theo bất kỳ xu hướng nào.
Khi sai số tăng hoặc giảm dần, mô hình bị phương sai thay đổi (heteroscedasticity). Cách khắc phục là chuẩn hóa hoặc biến đổi biến phụ thuộc, ví dụ dùng log(Y) thay cho Y để ổn định phương sai và tăng độ tin cậy.
5.5. Hồi quy logistic (Logistic Regression)
Mặc dù mang tên “hồi quy”, mô hình logistic lại được dùng cho bài toán phân loại, chứ không phải dự đoán giá trị liên tục, , đặc biệt thuộc nhóm Supervised Learning – Classification.
Công thức của hồi quy logistic có dạng:
P(Y=1) = 1 / (1 + e^(-z))
trong đó:
z = β₀ + β₁X₁ + β₂X₂ + … + βₙXₙ
- z là tổ hợp tuyến tính của các biến độc lập
- Hàm sigmoid biến đổi z thành xác suất từ 0 đến 1
Mô hình logistic được dùng trong học máy vì cho ra kết quả trả về là xác suất xảy ra của một sự kiện, nằm trong khoảng 0 đến 1. Cùng với đó, mô hình này hoạt động tốt ngay cả khi dữ liệu không quá lớn, và trở thành nền tảng trước khi tiến tới SVM, cây quyết định, random forest, hoặc mạng nơ-ron,…
Ví dụ:
- Xác suất khách hàng mua sản phẩm (marketing, e-commerce)
- Khả năng một bệnh nhân mắc bệnh tim (healthcare)
- Xác suất học sinh vượt qua kỳ thi (giáo dục)
- Phân loại email có phải spam hay không (an ninh mạng)
- Xác định giao dịch có gian lận hay không (fintech, ngân hàng)
6. FAQ – Câu hỏi thường gặp
1. Hồi quy tuyến tính là gì?
Hồi quy tuyến tính là mô hình thống kê mô tả mối quan hệ tuyến tính giữa biến phụ thuộc và biến độc lập, giúp phân tích và dự đoán dữ liệu.
2. Khi nào nên dùng hồi quy tuyến tính?
Khi dữ liệu có quan hệ tuyến tính và mục tiêu là dự đoán một biến dựa trên một hoặc nhiều biến khác.
3. Công thức hồi quy tuyến tính đơn là gì?
Y = β0 + β1X + ε
4. R² trong hồi quy tuyến tính có ý nghĩa gì?
R² cho biết mô hình giải thích được bao nhiêu phần trăm biến thiên của dữ liệu.
5. Nhược điểm lớn nhất của hồi quy tuyến tính là gì?
Mô hình dễ sai lệch nếu dữ liệu có outliers, không tuyến tính hoặc bị đa cộng tuyến giữa các biến độc lập.
Bài viết trên Tri Thức Cộng Đồng đã giúp bạn làm rõ khái niệm, bản chất và vai trò quan trọng của hồi quy tuyến tính trong phân tích dữ liệu cũng như trong các mô hình học máy hiện đại.
Thông qua những ví dụ trực quan, công thức cụ thể và ứng dụng thực tiễn, bạn có thể thấy rằng hồi quy tuyến tính không chỉ là một mô hình thống kê đơn giản mà còn là nền tảng vững chắc của khoa học dữ liệu và trí tuệ nhân tạo, giúp con người biến dữ liệu thô thành tri thức có giá trị và dự đoán chính xác hơn.

 14 Tháng 1, 2026
14 Tháng 1, 2026 Share
Share