Trong thống kê và phân tích dữ liệu, bên cạnh giá trị trung bình thì yếu tố quan trọng không kém là mức độ biến động của dữ liệu. Đó chính là lý do vì sao khái niệm độ lệch chuẩn luôn được quan tâm. Vậy độ lệch chuẩn là gì, công thức tính độ lệch chuẩn như thế nào và nó có ý nghĩa gì trong thực tế? Bài viết này sẽ giúp bạn hiểu rõ khái niệm, nắm vững cách tính kèm theo ví dụ minh họa cụ thể, từ đó dễ dàng áp dụng trong học tập, nghiên cứu và cả lĩnh vực tài chính, đầu tư.
1. Khái niệm độ lệch chuẩn
1.1. Độ lệch chuẩn là gì?
Độ lệch chuẩn (Standard Deviation) là một thước đo thống kê cho biết mức độ phân tán của dữ liệu so với giá trị trung bình. Nói cách khác, nó cho thấy các giá trị trong tập dữ liệu nằm gần hay xa so với trung bình.
- Nếu độ lệch chuẩn nhỏ, các giá trị tập trung gần nhau → dữ liệu ổn định, ít biến động.
- Nếu độ lệch chuẩn lớn, các giá trị phân tán rộng → dữ liệu biến động mạnh, khó dự đoán.
Khái niệm độ lệch chuẩn
Ví dụ:
- Nếu độ lệch chuẩn của điểm số của học sinh trong một lớp học là 5 điểm, điều đó có nghĩa là trung bình mỗi học sinh có điểm số lệch 5 điểm so với điểm trung bình của lớp.
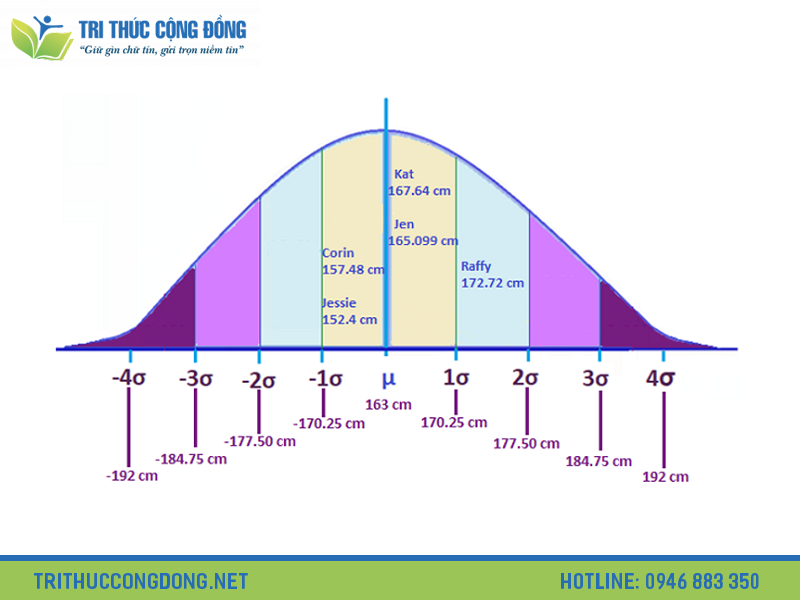
- Nếu độ lệch chuẩn của chiều cao của người dân trong một vùng là 10cm, điều đó có nghĩa là trung bình mỗi người có chiều cao lệch 10cm so với chiều cao trung bình của người dân trong vùng.
1.2. Vai trò của độ lệch chuẩn
Độ lệch chuẩn không chỉ là một công cụ tính toán trong thống kê, mà còn giữ vai trò quan trọng trong việc phân tích, so sánh và dự đoán dữ liệu. Khi kết hợp với công thức tính độ lệch chuẩn, chúng ta có thể đánh giá mức độ ổn định hoặc biến động trong nhiều lĩnh vực khác nhau:
- Phân tích dữ liệu: Độ lệch chuẩn giúp đánh giá mức độ phân tán của dữ liệu, cho phép nhà nghiên cứu đưa ra kết luận chính xác hơn về dữ liệu.
- Kiểm tra giả thuyết: Độ lệch chuẩn được sử dụng để kiểm tra giả thuyết thống kê, ví dụ như xác định xem sự khác biệt giữa hai nhóm dữ liệu có ý nghĩa thống kê hay không.
- Dự báo: Độ lệch chuẩn được sử dụng để dự báo tương lai, ví dụ như dự báo doanh thu của một công ty trong năm tới.
- Kiểm soát chất lượng: Độ lệch chuẩn được sử dụng để kiểm soát chất lượng sản phẩm, ví dụ như kiểm tra xem kích thước của một sản phẩm có phù hợp với tiêu chuẩn hay không.
>> Đọc thêm: Danh mục hình ảnh trong tiểu luận đẹp & chuẩn xác
1.3. Ý nghĩa của độ lệch chuẩn
Độ lệch chuẩn là một chỉ số quan trọng trong đầu tư và giao dịch tài chính, bởi nó phản ánh mức độ biến động của thị trường cũng như hỗ trợ dự đoán xu hướng giá.
Về bản chất, độ lệch chuẩn cho thấy sự khác biệt giữa giá trị quan sát tại từng thời điểm với mức trung bình trong giai đoạn phân tích. Khi giá đóng cửa lệch nhiều so với giá trung bình, chỉ số biến động và độ lệch chuẩn sẽ tăng cao. Ngược lại, nếu khoảng cách này nhỏ, cả biến động và độ lệch chuẩn đều ở mức thấp.
Trong thực tế, khi thị trường xuất hiện những biến động mạnh, nhà đầu tư thường nhận diện các điểm đảo chiều hình thành đáy hoặc đỉnh giá. Ngược lại, giai đoạn thị trường điều chỉnh hay đi ngang thường gắn liền với độ lệch chuẩn thấp, báo hiệu một xu thế mới có thể xuất hiện. Như vậy, dữ liệu giá biến động lớn sẽ tạo ra giá trị độ lệch chuẩn cao, còn dữ liệu giá ổn định sẽ phản ánh qua độ lệch chuẩn thấp.
2. Công thức tính độ lệch chuẩn
2.1. Công thức chung
Công thức tính độ lệch chuẩn được cho bởi:
s = √(∑(xᵢ – x̄)² / (n – 1))
Trong đó:
- s: Độ lệch chuẩn mẫu (Sample standard deviation)
- xᵢ: Giá trị của điểm dữ liệu thứ i
- x̄: Trung bình mẫu (Sample mean)
- n: Số lượng điểm dữ liệu trong mẫu
- ∑: Ký hiệu tổng
2.2. Công thức tính độ lệch chuẩn mẫu (Sample standard deviation)
Công thức tính độ lệch chuẩn mẫu (Sample standard deviation)
Công thức tính độ lệch chuẩn mẫu thường được sử dụng khi bạn cần tính độ lệch chuẩn của một mẫu dữ liệu. Công thức này sử dụng (n – 1) thay vì n ở mẫu số, để điều chỉnh độ lệch chuẩn mẫu cho phù hợp với độ lệch chuẩn của tổng thể.
>> Tham khảo thêm: Nhận làm tiểu luận thuê Hà Nội trọn gói, nhanh chóng
2.3. Công thức tính độ lệch chuẩn tổng thể (Population standard deviation)
Công thức tính độ lệch chuẩn tổng thể được sử dụng khi bạn biết tất cả các giá trị trong tổng thể. Công thức này sử dụng n thay vì (n – 1) ở mẫu số.
2.4. Ví dụ minh họa
Dưới đây là cách tính độ lệch chuẩn cho một tập hợp dữ liệu gồm 5 số:
| Số |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
- Bước 1: Tính trung bình mẫu (x̄):
(1 + 2 + 3 + 4 + 5) / 5 = 3
- Bước 2: Tính phương sai:
[(1 – 3)² + (2 – 3)² + (3 – 3)² + (4 – 3)² + (5 – 3)²] / (5 – 1) = 2
- Bước 3: Tính độ lệch chuẩn mẫu (s):
√2 ≈ 1.41
Kết luận: Độ lệch chuẩn của tập dữ liệu là 1.41, điều này cho thấy trung bình mỗi số trong tập hợp dữ liệu cách xa trung bình 1.41 đơn vị.
3. Mối quan hệ giữa độ lệch chuẩn và phương sai
3.1. Phương sai là gì?
Phương sai (variance) là bình phương của độ lệch chuẩn. Nó đo lường mức độ phân tán trung bình của dữ liệu so với trung bình.
3.2. Công thức tính phương sai
Công thức tính phương sai được cho bởi:
s² = ∑(xᵢ – x̄)² / (n – 1)
Trong đó:
- s²: Phương sai mẫu (Sample variance)
- xᵢ: Giá trị của điểm dữ liệu thứ i
- x̄: Trung bình mẫu (Sample mean)
- n: Số lượng điểm dữ liệu trong mẫu
- ∑: Ký hiệu tổng
3.3. Mối quan hệ giữa độ lệch chuẩn và phương sai
Độ lệch chuẩn và phương sai là hai đại lượng có mối quan hệ mật thiết. Phương sai là bình phương của độ lệch chuẩn, nghĩa là:
- Độ lệch chuẩn = √Phương sai
- Phương sai = Độ lệch chuẩn²
Ví dụ: Nếu độ lệch chuẩn của một tập dữ liệu là 3, thì phương sai của nó là 9 (3² = 9).
3.4. Lợi ích của việc sử dụng độ lệch chuẩn thay vì phương sai
Độ lệch chuẩn thường được sử dụng thay vì phương sai vì nó có đơn vị giống với dữ liệu gốc.
Lợi ích của việc sử dụng độ lệch chuẩn thay vì phương sai
Ví dụ:
- Nếu đơn vị của dữ liệu là mét, thì độ lệch chuẩn cũng sẽ có đơn vị là mét.
- Trong khi đó, phương sai sẽ có đơn vị là mét vuông.
Độ lệch chuẩn dễ hiểu hơn phương sai vì nó cho biết mức độ phân tán của dữ liệu theo đơn vị giống với dữ liệu gốc.
Tóm lại, để trả lời câu hỏi độ lệch chuẩn là gì? Đây là một khái niệm quan trọng trong thống kê, được sử dụng để đo lường mức độ phân tán của dữ liệu xung quanh giá trị trung bình. Nó giúp đánh giá mức độ rủi ro, phân tích dữ liệu, kiểm tra giả thuyết và dự báo tương lai. Hiểu rõ về độ lệch chuẩn và công thức tính toán là rất cần thiết cho những ai muốn làm việc với dữ liệu và đưa ra những quyết định dựa trên cơ sở khoa học.
Hy vọng những chia sẻ của Tri Thức Cộng Đồng sẽ hữu ích cho quá trình học tập của bạn. Ngoài ra, nếu bạn có nhu cầu sử dụng dịch vụ chạy thuê SPSS, vui lòng liên hệ ngay với chúng tôi để được hỗ trợ nhanh chóng nhé!
Thông tin liên hệ:
- Hotline: 094 688 3350
- Website: https://trithuccongdong.net/
- Email: ttcd.group@gmail.com
- Địa chỉ:
144 Xuân Thủy, Dịch Vọng Hậu, Cầu Giấy, Hà Nội
2 Võ Oanh, Phường 25, Bình Thạnh, Hồ Chí Minh
9 Đại lộ Temasek, Suntec Tower, Singapore

 14 Tháng 1, 2026
14 Tháng 1, 2026 Share
Share