Trong thế giới thống kê, “normal” là một thuật ngữ quen thuộc, thường xuyên xuất hiện trong các bài báo khoa học, nghiên cứu, phân tích dữ liệu. Tuy nhiên, đối với những người chưa tiếp xúc với ngành này, “normal” có thể là một khái niệm mơ hồ, khó hiểu. Bài viết này của Tri Thức Cộng Đồng sẽ giúp bạn hiểu rõ hơn về “normal là gì” trong thống kê, phân tích dữ liệu và ứng dụng thực tiễn của nó.
1. Định nghĩa “normal”: Normal là gì?
Trong tiếng Anh, từ normal có nghĩa là “bình thường”, “chuẩn mực”, hay “theo tiêu chuẩn chung”.
“Normal” trong thống kê đại diện cho một khái niệm quan trọng được gọi là phân phối chuẩn, hay còn gọi là phân phối Gauss. Phân phối chuẩn là một loại phân phối xác suất liên tục, được mô tả bởi một hàm toán học cụ thể.
1.1. Đặc điểm của phân phối chuẩn(Normal Distribution)
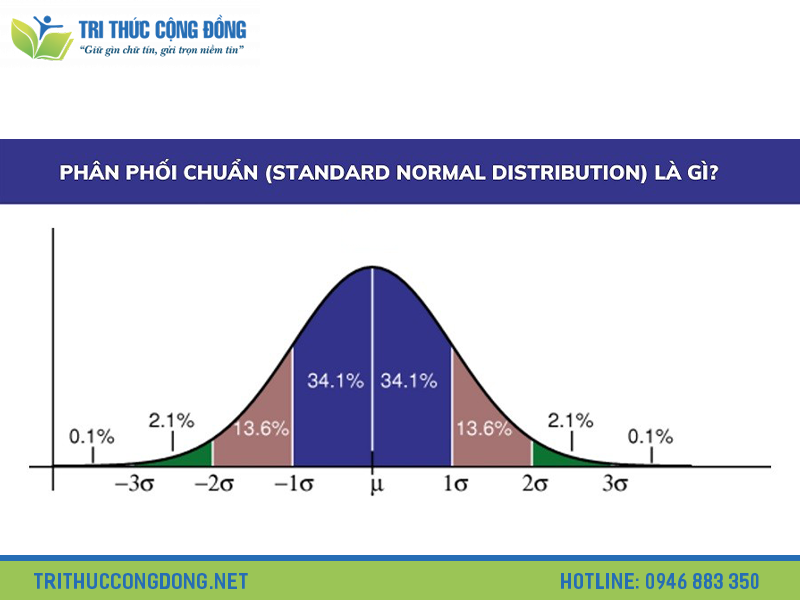
Đặc điểm của phân phối chuẩn
- Hình dạng: Đường cong phân phối chuẩn có hình dạng giống như một chuông, đối xứng về trục trung tâm tức giá trị trung bình μ.
- Trung bình, trung vị, mốt: Trong phân phối chuẩn, ba giá trị này trùng nhau.
- Độ lệch chuẩn: Độ lệch chuẩn xác định độ rộng của chuông(σ càng lớn → chuông càng rộng và dẹt, σ nhỏ → chuông càng hẹp và nhọn).
- Giá trị trung bình(μ) quyết định vị trí đường cong, còn độ lệch chuẩn(σ) quyết định mức độ phân tán.
- Tổng xác suất dưới đường cong luôn bằng 1.
- Phân phối chuẩn là kết quả của Định luật giới hạn trung tâm, theo đó trung bình của nhiều mẫu ngẫu nhiên độc lập (có phương sai hữu hạn) sẽ tiến gần đến phân phối chuẩn.
1.2. Tại sao phân phối chuẩn lại quan trọng?
Phân phối chuẩn đóng vai trò quan trọng trong thống kê vì:
- Sự phổ biến: Nhiều biến số trong thực tế tuân theo hoặc gần giống với phân phối chuẩn, bao gồm: chiều cao, cân nặng, điểm thi, huyết áp,…
- Dễ dàng sử dụng: Phân phối chuẩn có các tính chất toán học dễ dàng sử dụng, giúp cho việc tính toán và dự đoán trở nên đơn giản hơn.
- Ứng dụng rộng rãi: Phân phối chuẩn được sử dụng trong nhiều lĩnh vực như: y tế, kinh tế, kỹ thuật, xã hội,…
>> Đọc thêm: Phần mềm hỗ trợ viết luận văn tốt nhất hiện nay
1.3. Công thức tính phân phối chuẩn

Công thức tính phân phối chuẩn Normal Distribution
Trong đó:
- 𝑥: giá trị ngẫu nhiên (biến số cần xét)
- 𝜇: trung bình (mean) của phân phối
- 𝜎: độ lệch chuẩn (standard deviation)
- 𝜎2: phương sai (variance)
- 𝑒: hằng số Euler (≈ 2.718)
- 𝜋: số Pi (≈ 3.1416)
1.3. Ví dụ về Phân phối chuẩn Normal Distribution
Một công ty thực phẩm đang chuẩn bị đưa một loại bánh mới ra thị trường. Người ta nhận thấy rằng số ngày sử dụng tốt tối đa của mỗi chiếc bánh trong điều kiện khuyến cáo là BNN có phân phối chuẩn với trung bình là 15 ngày và phương sai 1,7 ngày 2. Xác suất loại bánh mới vẫn sử dụng được sau 18 ngày?
Giải:
Bước 1: Xác định tham số của Phân phối chuẩn
Phân phối chuẩn với trung bình là 15 ngày → 𝜇 = 15
Phương sai 1,7 → 𝜎2 = 1.7 → Độ lệch chuẩn 𝜎 = √1.7 ~ 1.304
X ~ N với 𝜇 = 15, 𝜎2 = 1.7
Bước 2: Chuẩn hóa về biến Z với X = 18

P (Z < 2.30) ~ 0.9893
Do đó:
P ( X> 18) = 1- P ( Z> 2.30) = 1- 0.9893 = 0,0107
Kết quả:
Xác suất chiếc bánh vẫn còn sử dụng được sau 18 ngày là khoảng:
P ( X> 18) ~ 0.0107( Tức khoảng 1,07 %)
2. Normal Distribution trong SPSS là gì?
SPSS (Statistical Package for the Social Sciences) là một phần mềm thống kê được sử dụng rộng rãi trong nghiên cứu khoa học. Trong SPSS, Normal Distribution là một chức năng giúp kiểm tra xem dữ liệu có tuân theo phân phối chuẩn hay không.
2.1. Kiểm tra tính phân phối chuẩn trong SPSS
SPSS cung cấp nhiều phương pháp để kiểm tra tính phân phối chuẩn, bao gồm:
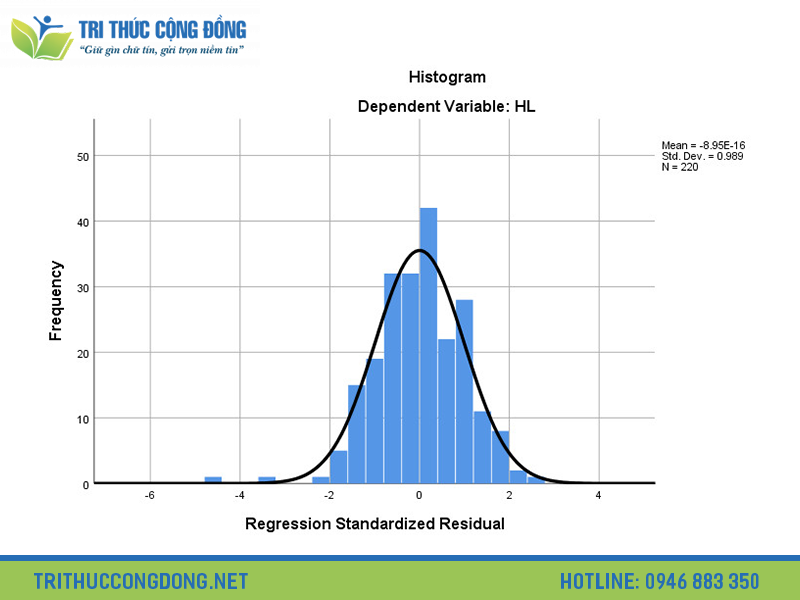
Normal Distribution trong SPSS là gì?
- Kiểm tra trực quan: Sử dụng biểu đồ tần số, biểu đồ boxplot, biểu đồ Q-Q plot để kiểm tra hình dạng và tính đối xứng của dữ liệu.
- Kiểm tra dựa trên thống kê: Sử dụng các chỉ số thống kê như Shapiro-Wilk test, Kolmogorov-Smirnov test,…
Kiểm tra tính phân phối chuẩn là cần thiết vì:
- Giúp đảm bảo độ tin cậy của kết quả thống kê: Nhiều phép thử thống kê đòi hỏi dữ liệu phải tuân theo phân phối chuẩn.
- Giúp lựa chọn phương pháp thống kê phù hợp: Nếu dữ liệu không tuân theo phân phối chuẩn, chúng ta cần sử dụng các phương pháp thống kê khác thay thế.
- Giúp hiểu rõ hơn về đặc điểm của dữ liệu: Kiểm tra tính phân phối chuẩn giúp chúng ta nhận biết được sự phân bố của dữ liệu và dự đoán xu hướng phát triển của nó.
>> Tham khảo thêm: Dịch vụ viết thuê tiểu luận uy tín cho sinh viên
2.2. Ví dụ về kiểm tra tính phân phối chuẩn Normal Distribution trong SPSS
Giả sử chúng ta muốn kiểm tra xem dữ liệu điểm số của học sinh trong một bài kiểm tra có tuân theo phân phối chuẩn hay không. Trong SPSS, ta có thể vẽ biểu đồ tần số (Histogram), biểu đồ Boxplot và thực hiện kiểm định Shapiro–Wilk. Nếu giá trị Sig. của kiểm định lớn hơn 0.05, ta kết luận dữ liệu có thể được xem là phân phối chuẩn. Khi đó, việc áp dụng các phương pháp thống kê tham số sẽ đảm bảo độ tin cậy cao hơn.
3. Cách sử dụng Normal Distribution như thế nào?
Phân phối chuẩn có nhiều ứng dụng trong thực tiễn, bao gồm:
3.1. Dự đoán các sự kiện
- Dùng trong dự báo: Dự đoán xu hướng phát triển của biến số dựa trên dữ liệu hiện có.
- Lập kế hoạch: Lập kế hoạch cho các dự án, sản xuất, kinh doanh dựa trên dự đoán về nhu cầu, tiêu thụ,…
- Kiểm soát chất lượng: Kiểm soát chất lượng sản phẩm, dịch vụ bằng cách xác định giới hạn kiểm soát cho các chỉ số chất lượng quan trọng.
3.2. Xây dựng các mô hình thống kê
- Mô hình hồi quy: Xây dựng các mô hình hồi quy để dự đoán mối quan hệ giữa các biến số độc lập và biến số phụ thuộc.
- Phân tích phương sai: Phân tích phương sai để tìm hiểu sự khác biệt giữa các nhóm đối tượng hoặc các phương pháp điều trị.
3.3. Phân tích dữ liệu
- Kiểm tra giả thuyết: Kiểm tra các giả thuyết thống kê dựa trên dữ liệu mẫu.
- Xây dựng khoảng tin cậy: Xây dựng khoảng tin cậy cho các tham số của phân phối.
4. Ví dụ thực tế về cách sử dụng Normal Distribution
4.1. Trong y tế
Phân phối chuẩn được sử dụng để xác định giới hạn bình thường cho các chỉ số sinh lý như huyết áp, nhiệt độ, đường huyết,…
Ví dụ:
- Chỉ số huyết áp tâm thu của người trưởng thành thường có phân phối gần chuẩn với trung bình khoảng 120 mmHg. Bác sĩ dựa vào phân phối chuẩn này để xác định “ngưỡng bình thường” và phát hiện bệnh nhân có nguy cơ tăng huyết áp.
4.2. Trong sản xuất
Phân phối chuẩn được sử dụng để kiểm soát chất lượng của các sản phẩm, xác định giới hạn kiểm soát cho các chỉ số chất lượng quan trọng.
Ví dụ:
- Một nhà máy sản xuất linh kiện điện tử kiểm soát chất lượng sản phẩm bằng cách đo đường kính của trục thép. Kết quả đo tuân theo phân phối chuẩn, cho phép kỹ sư xác định giới hạn kiểm soát (±3σ). Nếu sản phẩm nằm ngoài phạm vi này, nó được xem là lỗi và loại bỏ.
4.3. Trong kinh tế
Phân phối chuẩn được sử dụng để dự đoán xu hướng thị trường chứng khoán, dự báo sản lượng, lợi nhuận,…
Ví dụ:
- Nhà phân tích chứng khoán giả định lợi suất ngày của một cổ phiếu tuân theo phân phối chuẩn với trung bình 0.2% và độ lệch chuẩn 1%. Từ đó, họ có thể ước tính xác suất lợi suất giảm quá 2% trong một ngày, hỗ trợ việc quản trị rủi ro đầu tư.
5. Tri Thức Cộng Đồng nhận xử lý và chạy SPSS uy tín
Để tận dụng tối đa ưu điểm của phân phối chuẩn và SPSS, bạn có thể tìm đến Tri Thức Cộng Đồng, một đơn vị cung cấp dịch vụ phân tích dữ liệu chuyên nghiệp, đáng tin cậy.
5.1. Dịch vụ của Tri Thức Cộng Đồng

Tri Thức Cộng Đồng nhận xử lý và chạy SPSS uy tín
- Phân tích dữ liệu SPSS: Chạy các phép thử thống kê, tạo bảng biểu, đồ thị minh họa, báo cáo, phân tích kết quả.
- Kiểm tra tính phân phối chuẩn: Kiểm tra dữ liệu có tuân theo phân phối chuẩn hay không.
- Tư vấn và hỗ trợ: Cung cấp tư vấn về phương pháp phân tích dữ liệu phù hợp với nhu cầu của bạn.
- Hỗ trợ kỹ thuật: Hỗ trợ kỹ thuật sử dụng SPSS, giải đáp các vấn đề bạn gặp phải.
5.2. Ưu điểm của dịch vụ
- Chuyên nghiệp và uy tín: Tri Thức Cộng Đồng được thành lập bởi các chuyên gia có trình độ chuyên môn cao, kinh nghiệm phong phú trong lĩnh vực phân tích dữ liệu.
- Dịch vụ chất lượng cao: Cam kết mang đến cho khách hàng dịch vụ chất lượng cao, chính xác, hiệu quả.
- Giá cả hợp lý: Cung cấp dịch vụ với giá cả hợp lý, phù hợp với nhu cầu và kinh phí của bạn.
“Normal” là một khái niệm quan trọng trong thống kê. Hiểu rõ về phân phối chuẩn, cách kiểm tra tính phân phối chuẩn và cách ứng dụng phân phối chuẩn trong SPSS giúp bạn khai thác tối đa thông tin từ dữ liệu, đưa ra các quyết định chính xác và hiệu quả hơn. Tri Thức Cộng Đồng là địa chỉ tin cậy hỗ trợ bạn trong việc phân tích dữ liệu, giải quyết các vấn đề liên quan đến thống kê.
Thông tin liên hệ:
- Hotline: 094 688 3350
- Website: https://trithuccongdong.net/
- Email: ttcd.group@gmail.com
- Địa chỉ:
144 Xuân Thủy, Dịch Vọng Hậu, Cầu Giấy, Hà Nội
2 Võ Oanh, Phường 25, Bình Thạnh, Hồ Chí Minh
9 Đại lộ Temasek, Suntec Tower, Singapore

 14 Tháng 1, 2026
14 Tháng 1, 2026 Share
Share