Kiểm định phi tham số - Khái niệm và 4 loại phổ biến nhất

Trong thực tế, các số liệu đôi khi chỉ biểu hiện dưới hình thức xếp hạng hoặc hình thức dấu. Vì vậy không phải lúc nào chúng ta cũng có thể sử dụng kiểm định tham số. Những trường hợp này cần sử dụng kiểm định phi tham số. Bạn đã biết khái niệm, cách dùng và các loại kiểm định phi tham số thường gặp chưa? Nếu chưa hãy đọc bài viết sau ngay nhé.

1. Khái niệm về kiểm định phi tham số

• Khái niệm

Kiểm định phi tham số trong tiếng anh là nonparametric tests. Đây là một phương pháp toán học thường được sử dụng trong kiểm định giả thuyết thống kê không đưa ra giả định về phân bố tần suất của các biến sẽ được đánh giá. 

• Sử dụng cho trường hợp

Kiểm định phi tham số thường được sử dụng trong những trường hợp mẫu hoặc dữ liệu nhỏ có ít quan sát hoặc không có phân phối chuẩn. 

Loại kiểm định này cũng được dùng cho các dữ liệu thứ bậc - ordinal, dữ liệu định danh - nominal hoặc dữ liệu khoảng cách - interval có phân phối bất kì.

• Đặc điểm nổi bật của kiểm định phi tham số

Từ không tham số không có nghĩa là các mô hình này không có bất kỳ tham số nào. Thực tế là, các đặc điểm và số lượng tham số khá linh hoạt và không được xác định trước.

Khi sử dụng kiểm định này khả năng tìm ra được sự sai biệt kém, không mạnh như các pháp kiểm định có tham số khác và khó mở rộng để giải quyết các mô hình kinh tế phức tạp hơn.

2. Phân biệt 4 loại kiểm định phi tham số phổ biến

2.1. Kiểm định dấu (Sign test)

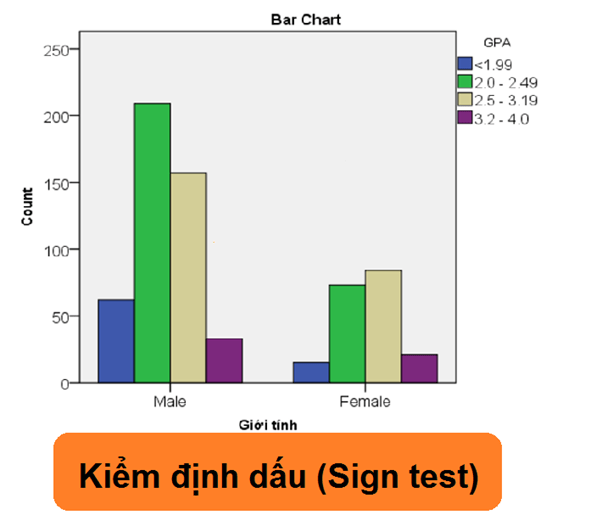
Kiểm định dấu (Sign test)

• Khái niệm

Kiểm định dấu là thủ tục phi tham số đơn giản nhất được sử dụng cho 2 mẫu có quan hệ với nhau. Trong kiểm định dấu chúng ta không quan tâm đến thứ hạng chỉ ghi nhận ấu âm (-), dương (+).

• Sử dụng cho trường hợp

Kiểm định dấu dùng để kiểm định về giá trị trung vị của một tổng thể.

Kiểm định dấu dùng để kiểm định giả thuyết với hai mẫu tương đồng từng cặp

2.2. Kiểm định dấu và hạng Wilcoxon

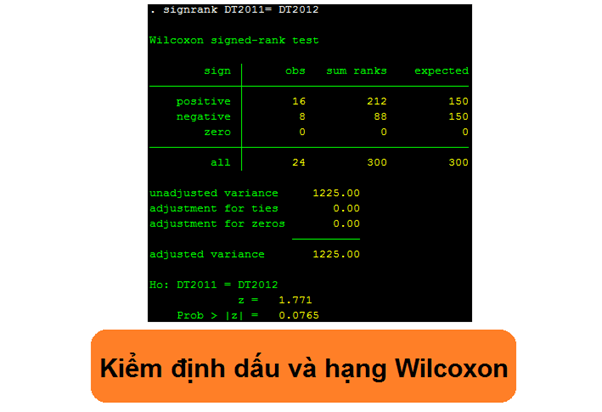
Kiểm định dấu và hạng Wilcoxon

• Khái niệm

Kiểm định Wilcoxon (Signed-rank test) là một dạng kiểm tra giả thuyết thống kê phi tham số được sử dụng để kiểm tra vị trí của tập hợp mẫu hoặc để so sánh hai vị trí của quần thể có liên quan bằng cách sử dụng một tập hợp mẫu phù hợp.

• Sử dụng cho trường hợp

Kiểm định dấu và hạng Wilcoxon dùng trong 3 trường hợp: mẫu không đủ lớn, người tham gia có những đặc điểm giống nhau hoặc thử nghiệm được thực hiện 2 lần hay trong 2 điều kiện khác nhau trên cùng một biến phụ thuộc.

2.3. Kiểm định Mann-Whitney

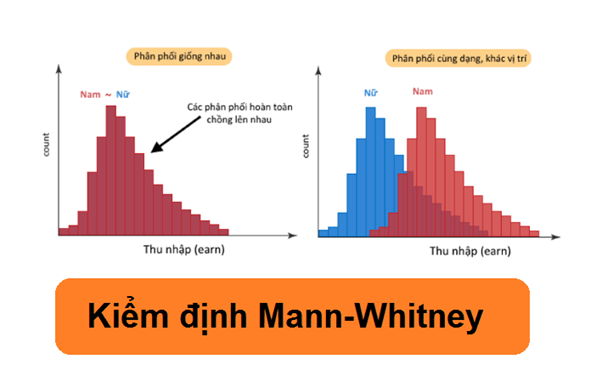
Kiểm định Mann-Whitney

• Khái niệm

Kiểm định Mann-Whitney là một trong những kiểm định dựa trên xếp hạng. Các quan sát sẽ được xếp hạng từ giá trị nhỏ nhất tới lớn nhất và sau đó thứ hạng sẽ được sử dụng thay cho các giá trị thực trong tính toán.

• Sử dụng cho trường hợp

Kiểm định Mann-Whitney U dùng để kiểm định liệu có tồn tại sự khác biệt giữa hai tổng thể, với điều kiện:

- Tổng thể không có phân phối chuẩn;

- Dữ liệu ít nhất phải có thang đo thứ bậc;

- Hai mẫu được chọn ngẫu nhiên độc lập với nhau.

Giả thuyết cần kiểm định:  H0: Phân phối của hai tổng thể là giống hệt nhau (μ1= μ2).

2.4. Kiểm định Kruskal - Wallis

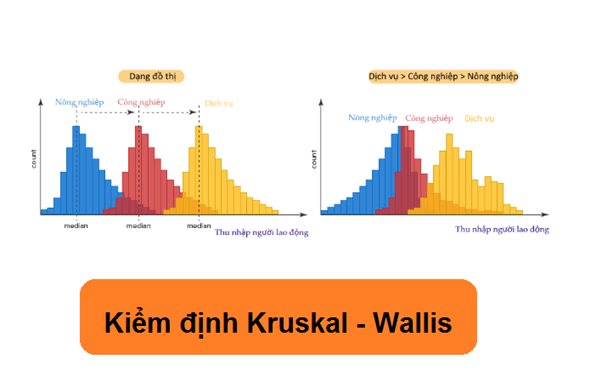
Kiểm định Kruskal - Wallis

• Khái niệm

Kiểm định Kruskal - Wallis là một giải pháp kiểm định được sử dụng để so sánh sự khác biệt về giá trị trung bình của một biến phụ thuộc theo hai hay nhiều chiều của biến độc lập, nhưng không bắt buộc biến phụ thuộc này phải phân phối chuẩn.

• Sử dụng cho trường hợp

Kiểm định Kruskal - Wallis được sử dụng khi các biến phụ thuộc và độc lập trong tập dữ liệu phải đáp ứng những điều kiện sau:

- Biến độc lập: là biến phân loại hai mức trở lên.

- Biến phụ thuộc: phải là biến thứ tự hoặc biến liên tục, không yêu cầu cần phải có phân phối chuẩn trong từng nhóm.

Đội ngũ của Tri Thức Cộng Đồng luôn lắng nghe, tư vấn tận tình cho từng khách hàng về dịch vụ nhận chạy mô hình spss, giảm bớt nỗi lo về thời gian, chi phí mà vẫn hoàn thành bài đúng thời hạn.

Sau khi đọc bài viết trên bạn đã hiểu rõ khái niệm cũng như ứng dụng của các loại kiểm định phi tham số. Hy vọng những kiến thức bổ ích này sẽ giúp bạn hoàn trình quá trình học tập tốt hơn.