Hệ Số Tương Quan Pearson Trong Spss: Định Nghĩa, Công Thức, Các Bước

Hệ số tương quan Pearson là phương pháp xử lý số liệu được rất nhiều người dùng ưa chuộng bởi tính chính xác và kết quả nhanh gọn mà nó mang lại. Ở bài viết này, Tri thức Cộng đồng sẽ giúp bạn tìm hiểu về hệ số tương quan Pearson trong spss cùng với công thức tính, cách phân tích và ví dụ cụ thể để bạn thực chiến trên chính dữ liệu có sẵn của mình. 

Hệ số tương quan Pearson là gì trong spss?

Mục lục

• 1. Định nghĩa hệ số tương quan pearson
• 2. Công thức tính 
• 3.  Ý nghĩa hệ số tương quan pearson
• 4. Ví dụ tình huống phân tích
• 5. Phân tích hệ số tương quan pearson SPSS với 3 bước 
• 6. Đọc ý nghĩa hệ số Pearson đã phân tích

1. Định nghĩa hệ số tương quan pearson

Hệ số tương quan Pearson còn được gọi là hệ số Pearson (Pearson Correlation Coefficient) trong thống kê được định nghĩa là thước đo mối quan hệ thống kê giữa hai biến và sự liên kết của chúng với nhau. 

Hệ số tương quan sẽ trả lời cho những câu hỏi như: 

• Có mối quan hệ tương quan nào giữa áp lực và năng suất công việc? 
• Có mối quan hệ tương quan nào giữa hương vị của món ăn và giá cả bạn phải trả,... 

Có vô vàn những thắc mắc kiểu như vậy được đặt ra, và hệ số tương quan Pearson sẽ giúp bạn làm sáng tỏ mối quan hệ giữa các biến như thế.

Hệ số tương quan Pearson ngày nay được coi là một trong những phương pháp được ưa chuộng nhất để đo lường mối quan hệ giữa các biến. Nó cung cấp cho chúng ta những thông tin quan trọng của các biến, về mối liên hệ giữa các biến, về tương quan và cả hướng phát triển của mối quan hệ ấy.

Đọc thêm:

• Kiểm định phi tham số spss
• Kiểm định wilcoxon
• Kiểm định mann-whitney

2. Công thức tính 

Cũng như các phương thức thống kê khác trong phần mềm spss thì hệ số tương quan Pearson cũng có công thức tính như sau:

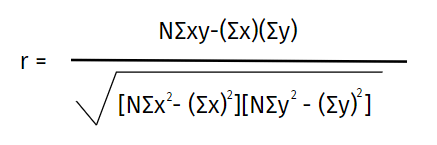
Công thức tính

Trong đó: 

N: Số cặp điểm

Σxy = tổng các tích của các điểm được ghép nối

Σx = tổng điểm x

Σy = tổng điểm y

Σx2 = tổng điểm x bình phương

Σy2 = tổng điểm y bình phương

Sau khi đã có công thức tính, Tri thức Cộng đồng hướng dẫn bạn áp dụng công thức vào thực hành cụ thể bằng các bước dưới đây: 

Bước 1: Tạo bảng hệ số tương quan Pearson

Lập biểu đồ dữ liệu, bao gồm cả các biến. Gắn nhãn các biến này là ‘x’ và ‘y.’ Thêm ba cột bổ sung - (xy), (x ^ 2) và (y ^ 2). Tham khảo biểu đồ dữ liệu đơn giản này.

Tạo bảng hệ số tương quan Pearson

Bước 2: Tính toán giá trị các biến  

Sử dụng phép nhân cơ bản để hoàn thành bảng. 

Tính toán giá trị các biến  

Bước 3: Cộng tổng giá trị các biến 

Cộng tất cả các cột từ dưới lên trên.

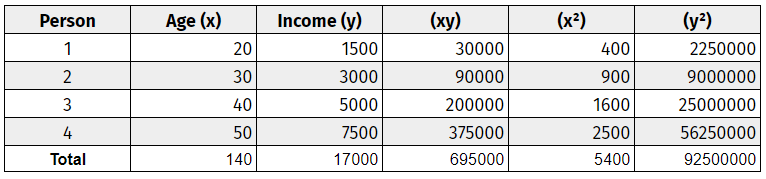
Cộng tổng giá trị các biến 

Bước 4: Bổ sung giá trị các biến 

Sử dụng công thức tương quan để bổ sung các giá trị.

• Nếu kết quả các biến là âm, có mối quan hệ tương quan nghịch đảo giữa hai biến. 
• Nếu kết quả là dương, có mối quan hệ tương quan thuận chiều giữa các biến. 

Kết quả cũng có thể xác định độ mạnh của mối quan hệ tuyến tính, tức là mối quan hệ tích cực mạnh, mối quan hệ tiêu cực mạnh, mối quan hệ tích cực trung bình, v.v.

Dù đã đọc rất nhiều thông tin cũng như hướng dẫn cụ thể về việc xử lý dữ liệu bằng phần mềm spss nhưng không phải ai cũng thông thạo thực hành ngay lập tức. Nếu bạn đang gặp khó khăn trong việc phân tích số liệu hay không biết xử lý số liệu như thế nào cho nhanh nhất, hiệu quả nhất thì hãy tham khảo ngay dịch vụ thuê xử lý số liệu spss của Trung tâm Tri Thức Cộng Đồng. Với đội ngũ chuyên viên giàu kinh nghiệm xử lý hơn 10.000 bộ dữ liệu cho hơn 15.000 khách hàng đến từ mọi lĩnh vực, chắc chắn sẽ không làm bạn thất vọng. 

3.  Ý nghĩa hệ số tương quan pearson

Mỗi biến và mỗi giá trị trong hệ số tương quan Pearson đều mang một ý nghĩa khác nhau, thể hiện đúng chức năng của nó. 

Ý nghĩa hệ số tương quan:

Thông thường, tương quan Pearson có giá trị biến động trong khoảng từ -1 đến +1.

• Với r = 0: Hai biến trong hệ số không có quan hệ tương quan tuyến tính
• Với r = 1 hoặc r = -1: Hai biến trong hệ số có quan hệ tương quan tuyến tính tuyệt đối.
• Nếu r <0: Hệ số tương quan âm. Điều này đồng nghĩa với việc giá trị 2 biến phụ thuộc sẽ đối lập nhau. Giá trị biến x giảm thì giá trị biến y tăng và ngược lại, giá trị biến x tăng thì giá trị biến y giảm. 
• Nếu r >0: Hệ số tương quan dương. Điều này đồng nghĩa với việc giá trị 2 biến phụ thuộc nhau song hành nhau. Giá trị biến x tăng thì giá trị biến y tăng và ngược lại, giá trị biến y tăng thì giá trị biến x cũng tăng theo. 

Lưu ý giá trị các biến:

• r nằm trong khoảng từ 0,05 đến đến ± 1, các biến có mối quan hệ tương quan mạnh.
• r nằm trong khoảng từ 0,30 đến ± 0,49, các biến có mối quan hệ tương quan trung bình.
• r nằm dưới ± 29, các biến có mối quan hệ tương quan yếu.
• Trên đồ thị Scatter, nếu r = -1 dữ liệu các biến sẽ phân bổ trên một đường thẳng với độ dốc âm, r = 1 dữ liệu sẽ phân bổ trên một đường thẳng với độ dốc dương.
• Hệ số tương quan Pearson chỉ có ý nghĩa khi và chỉ khi mức ý nghĩa lớn hơn mức ý nghĩa quan sát, có nghĩa là α = 5% > sig. 

4. Ví dụ tình huống phân tích

Để hình dung rõ hơn về hệ số tương quan được phân tích như thế nào, chúng tôi ứng dụng vào một trường hợp cụ thể với tập dữ liệu được lấy trực tiếp từ trang web “Philosophy experiments”. 

Đề bài: Hợp lệ hay không hợp lệ?

Nội dung: Bài tập là một bài kiểm tra logic yêu cầu mọi người xác định xem các lập luận là “valid” hay “Invalid”. Dưới đây là bảng dữ liệu hoàn chỉnh. Chúng tôi quan tâm đến hai biến “Time” và “Score”. 

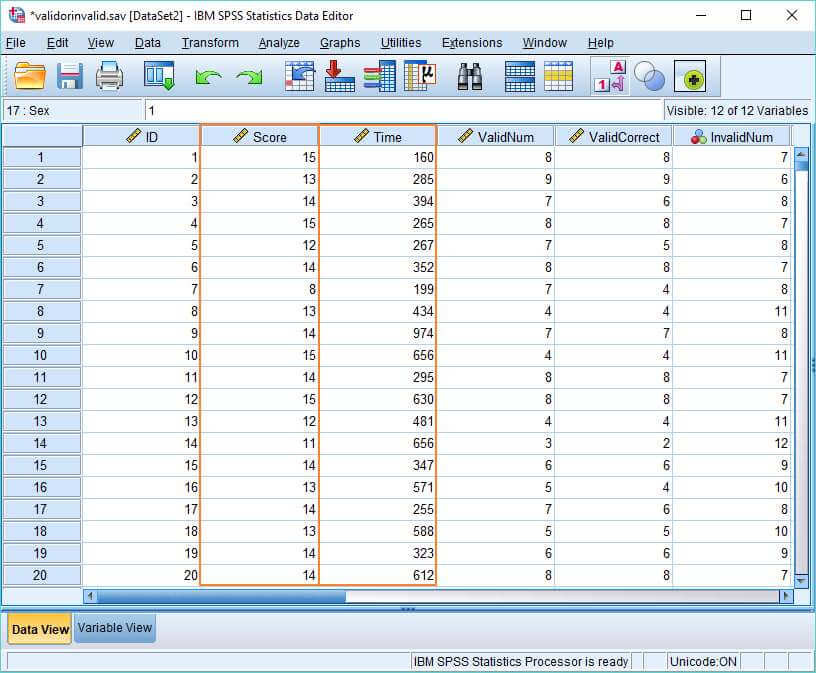
Ví dụ tình huống phân tích

Trong đó: 

• “Score” là minh chứng cho điểm số câu hỏi mà mọi người trả lời đúng. 
• “Time” là khoảng thời gian tính bằng giây mà họ cần để hoàn thành bài kiểm tra. 

Muốn tìm hiểu xem hai biến này có mối quan hệ tương quan với nhau hay không. Nói một cách đơn giản, mọi người có nhận được nhiều câu hỏi hơn nếu họ mất nhiều thời gian hơn để trả lời mỗi câu hỏi? Liệu thời gian bỏ ra để trả lời câu hỏi có tương quan với kết quả thu về hay không? 

Hệ số tương quan của Pearson sẽ giúp chúng ta trả lời câu hỏi này.

5. Phân tích hệ số tương quan pearson SPSS với 3 bước 

Hệ số tương quan Pearson bằng phần mềm SPSS được phân tích bằng 3 bước cụ thể dưới đây: 

Bước 1: Thiết lập biến 

Nhấp vào Analyze > Correlate > Bivariate.

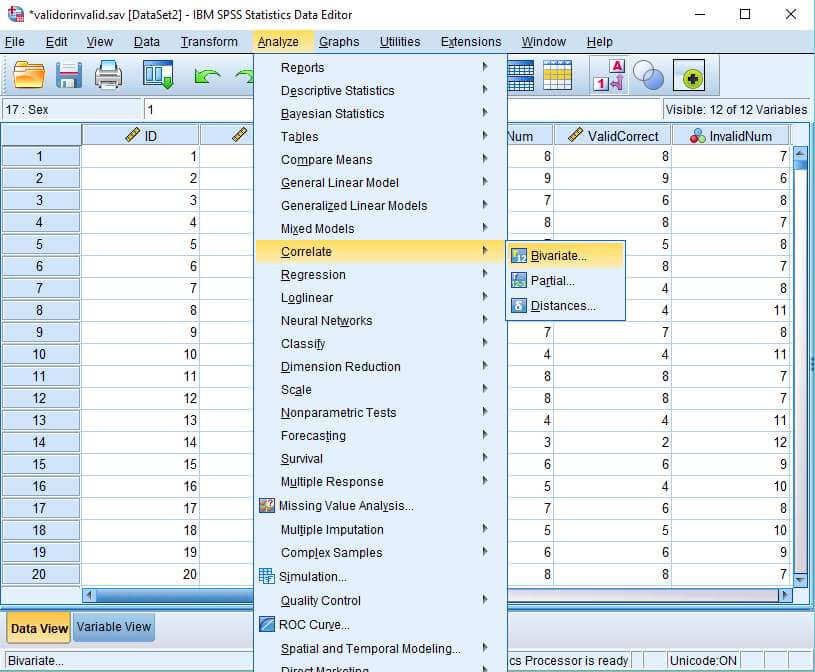
Thiết lập biến 

Bước 2: Di chuyển các biến 

Tại Cửa sổ Bivariate Correlations > Di chuyển hai biến bạn muốn kiểm tra sang hộp Biến ở bên phải

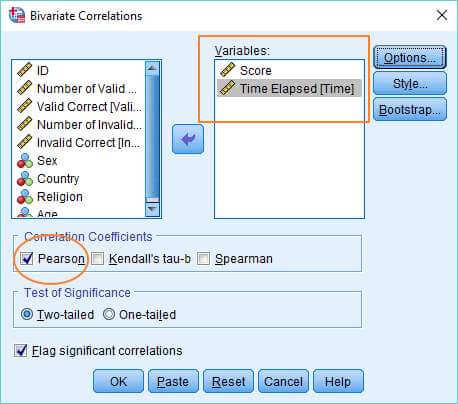
Di chuyển các biến 

Bước 3: Hoàn thành 

Nhấn OK để hoàn thành quá trình. 

Trên đây là 3 bước phân tích hệ số tương quan Pearson gắn liền với ví dụ có dữ liệu biến xác định để bạn dễ hình dung và thực hành theo. Mọi bước sẽ trở nên đơn giản hơn khi được sử dụng thông qua phần mềm spss. 

6. Đọc ý nghĩa hệ số Pearson đã phân tích

Sau khi đã áp dụng các biến trên vào công thức cụ thể thì kết quả sẽ thu được như phân tích dưới đây. 

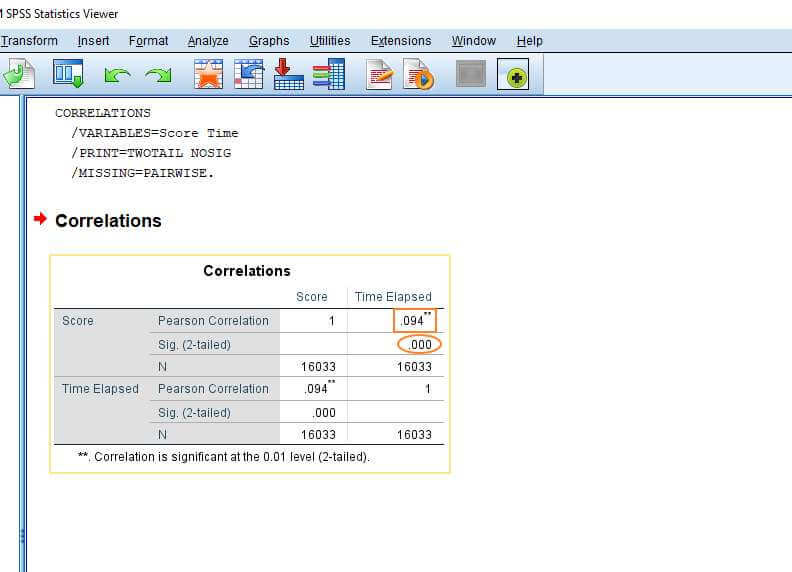
Đọc ý nghĩa hệ số Pearson đã phân tích

Chúng tôi quan tâm đến hai phần của kết quả là biến “Time” và “Score”. 

• Đầu tiên là giá trị của Pearson - tức là hệ số tương quan giữa các biến, trong trường hợp này là 0,94.
• Pearson có sự thay đổi giữa +1 và -1, trong đó +1 là hệ số tương quan dương hoàn hảo và -1 là hệ số tương quan âm hoàn hảo. 0 có nghĩa là không có tương quan tuyến tính nào cả.
• Con số 0,94 như ở bảng cho thấy mối tương quan thuận rất yếu. Điều này chứng tỏ một điều, mọi người càng dành nhiều thời gian để làm bài kiểm tra, thì khả năng họ làm được nhiều câu hỏi tăng cao, nhưng kết quả thu được lại là rất kém.

Trên đây là toàn bộ những thông tin chi tiết mà Tri thức cộng đồng chia sẻ về hệ số tương quan pearson trong spss là gì, công thức tính, các bước làm chi tiết đi kèm với ví dụ minh hoạ cụ thể mà chúng tôi tìm hiểu được để giúp bạn thuận lợi trong quá trình xử lý và làm gọn bộ số liệu của mình. Mọi khó khăn về xử lý số liệu sẽ trở nên đơn giản hơn khi bạn có thể áp dụng nhuần nhuyễn phương pháp này.