Mô hình hồi quy tuyến tính là một trong những phương pháp nghiên cứu thường được sử dụng để xác định mối quan hệ giữa một biến phụ thuộc và các biến độc lập. Với phần mềm SPSS, việc chạy mô hình hồi quy rất đơn giản và dễ dàng. Trong bài viết này, hãy cùng Tri Thức Cộng Đồng tìm hiểu về cách chạy mô hình hồi quy trong SPSS nhé!
1. Lý thuyết hồi quy tuyến tính trong SPSS
Hồi quy tuyến tính trong SPSS là phương pháp dự đoán giá trị của biến phụ thuộc (outcome) dựa vào giá trị của một hay nhiều biến độc lập (predictors). Thông qua mô hình hồi quy tuyến tính, chúng ta có thể tìm ra mối quan hệ giữa biến độc lập và biến phụ thuộc, từ đó đưa ra các kết luận và dự đoán.

Lý thuyết hồi quy tuyến tính trong SPSS
Mô hình hồi quy tuyến tính trong SPSS có dạng:
Y = β0 + β1X1 + β2X2 + … + βpXp + ε
Trong đó:
- Y: giá trị của biến phụ thuộc (outcome)
- X1, X2, …, Xp: giá trị của các biến độc lập (predictors)
- β0, β1, β2, …, βp: hệ số ước lượng (estimated coefficients) cho từng biến độc lập
- ε: sai số ngẫu nhiên (residuals)
Mục tiêu của mô hình hồi quy tuyến tính là tìm ra các hệ số ước lượng sao cho sai số ngẫu nhiên (ε) là nhỏ nhất. Để thực hiện việc này, chúng ta sử dụng phương pháp bình phương tối thiểu (least squares method) để ước lượng hệ số.
>> Đọc thêm: Cách chạy SPSS nghiên cứu khoa học chính xác
2. Hướng dẫn cách chạy mô hình hồi quy trong SPSS
Để chạy mô hình hồi quy trong SPSS, chúng ta có thể làm theo các bước sau:
- Bước 1: Chuẩn bị dữ liệu:
Trước khi thực hiện cách chạy mô hình hồi quy trong SPSS, bạn cần chuẩn bị dữ liệu cho phù hợp. Dữ liệu cần được nhập vào SPSS theo đúng định dạng và phải không chứa giá trị rỗng (missing values). Ngoài ra, để xác định được biến phụ thuộc và các biến độc lập, chúng ta cần có kiến thức về dữ liệu và mối quan hệ giữa các biến. (Tham khảo thêm Cách nhập dữ liệu vào SPSS).
- Bước 2: Mở bảng tính trong SPSS:
Sau khi đã chuẩn bị dữ liệu, bạn hãy chạy phần mềm SPSS và mở bảng tính (worksheet) tương ứng với dữ liệu của chúng ta.
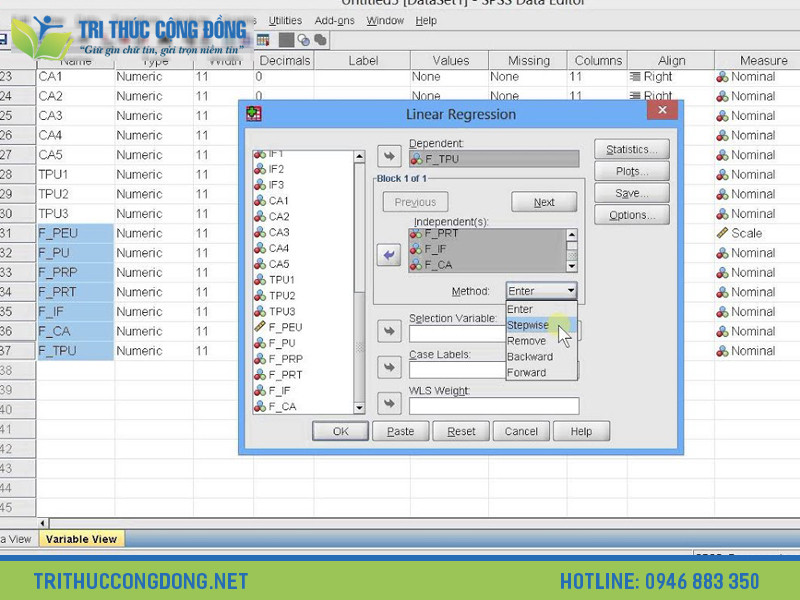
- Bước 3: Chọn menu Analyze và chọn Linear Regression:
Trong giao diện của SPSS, bạn chọn vào menu Analyze và chọn Linear Regression.
- Bước 4: Thiết lập biến phụ thuộc và các biến độc lập:
Tại cửa sổ Linear Regression, bạn hãy chọn biến phụ thuộc (Dependent) và các biến độc lập (Independent) cho mô hình hồi quy. Bạn có thể chọn nhiều biến độc lập bằng cách nhấn giữ phím Ctrl khi chọn các biến. Ở đây, Tri Thức Cộng Đồng sử dụng ví dụ về mô hình hồi quy tuyến tính đơn giản với một biến phụ thuộc và một biến độc lập. Biến phụ thuộc là “Điểm số” (Score) và biến độc lập là “Thời gian học” (Study Time).
- Bước 5: Thiết lập options cho mô hình hồi quy:
Tại phần Linear Regression, bạn có thể thiết lập options cho mô hình hồi quy như sau:
- Method: chọn Enter nếu muốn đưa tất cả các biến vào mô hình, chọn Backward hoặc Forward để loại bỏ các biến không cần thiết.
- Statistic: chọn các chỉ số thống kê bạn muốn hiển thị.
- Plots: chọn biểu đồ bạn muốn hiển thị.
- Bước 6: Nhấn nút OK và xem kết quả:
Sau khi đã thiết lập options cho mô hình hồi quy, bạn nhấn nút OK để SPSS chạy mô hình. Kết quả của mô hình hồi quy sẽ được hiển thị trong cửa sổ Output.
3. Đọc kết quả hồi quy tuyến tính trong phần mềm SPSS
Kết quả của mô hình hồi quy tuyến tính trong SPSS bao gồm các thông tin sau:
Kết quả của mô hình hồi quy tuyến tính trong SPSS
4. ANOVA
Trong phần ANOVA, bạn có thể xem tổng quan về mô hình hồi quy, bao gồm:
- F: giá trị F-statistic cho mô hình.
- Sig.: giá trị p-value cho F-statistic.
- R Square: tỉ lệ biến thiên của biến phụ thuộc được giải thích bởi các biến độc lập (tỷ lệ phần trăm của tổng sai số giữa quan sát và giá trị dự đoán).
- Adjusted R Square: R Square đã điều chỉnh dựa trên số lượng biến độc lập.
4.1. Coefficients
Phần Coefficients cho bạn biết về giá trị của hệ số ước lượng cho từng biến độc lập. Các thông tin chính như sau:
- Unstandardized Coefficients: giá trị ước lượng của hệ số β cho mỗi biến độc lập.
- Standard Error: độ lệch chuẩn của ước lượng hệ số.
- t: giá trị t-statistic cho hệ số.
- Sig.: giá trị p-value cho t-statistic.
- 95% Confidence Interval: khoảng tin cậy 95% cho ước lượng của hệ số.
4.2. Residuals
Phần Residuals cho người dùng biết về sai số ngẫu nhiên (ε) của mô hình hồi quy, bao gồm:
- Predicted Value: giá trị dự đoán của biến phụ thuộc.
- Std. Error of Predicted Y: độ lệch chuẩn của giá trị dự đoán.
- Residual: giá trị sai số (hiệu giữa giá trị thực tế và giá trị dự đoán).
- Std. Residual: giá trị sai số chuẩn hóa.
- Stud. Residual: giá trị sai số chuẩn hóa theo Studentized residual.
5. Ý nghĩa của các chỉ số trong hồi quy SPSS
Để hiểu rõ hơn về ý nghĩa của các chỉ số trong mô hình hồi quy tuyến tính, hãy cùng tìm hiểu chi tiết từng chỉ số như sau:
5.1. F-statistic và p-value
F-statistic là giá trị kiểm định F cho mô hình hồi quy và p-value là giá trị xác suất liên quan đến F-statistic. Giá trị F-statistic được tính bằng tỷ lệ sự biến thiên giữa mô hình hồi quy và sai số ngẫu nhiên. Nếu giá trị F-statistic cao và p-value thấp (thường được xem là p < 0.05), bạn có thể kết luận rằng mô hình hồi quy đó giải thích được một phần lớn sự biến thiên của biến phụ thuộc.
F-statistic và p-value
Tuy nhiên, giá trị F-statistic không cho biết thông tin về mức độ quan trọng của từng biến độc lập. Do đó, bạn cần phải xem xét các hệ số ước lượng để hiểu rõ hơn về mối quan hệ giữa biến phụ thuộc và các biến độc lập.
5.2. R Square và Adjusted R Square
R Square là tỉ lệ biến thiên của biến phụ thuộc được giải thích bởi các biến độc lập. Giá trị R Square càng cao, tức là mô hình hồi quy càng giải thích được nhiều phần trăm biến thiên của biến phụ thuộc. Tuy nhiên, R Square có thể bị ảnh hưởng bởi số lượng biến độc lập trong mô hình. Vì vậy, bạn cần phải sử dụng Adjusted R Square để điều chỉnh giá trị R Square. Giá trị Adjusted R Square đã điều chỉnh giảm mức độ tổng sai số do sự thêm vào của các biến độc lập không đóng góp cho mô hình hồi quy.
5.3. Hệ số ước lượng
Hệ số ước lượng (Unstandardized Coefficients) là giá trị ước lượng cho từng biến độc lập. Giá trị này thể hiện mức độ ảnh hưởng của biến độc lập đến biến phụ thuộc. Nếu hệ số ước lượng dương, thì khi biến độc lập tăng thì giá trị của biến phụ thuộc cũng tăng. Nếu hệ số ước lượng âm, thì khi biến độc lập tăng thì giá trị của biến phụ thuộc giảm.
5.4. Giá trị p-value của hệ số ước lượng
Giá trị p-value cho hệ số ước lượng được sử dụng để kiểm định xem liệu tác động của các biến độc lập có ý nghĩa thống kê đối với biến phụ thuộc hay không. Nếu giá trị p-value nhỏ hơn hoặc bằng mức ý nghĩa α (thường là α = 0,05), người dùng có thể kết luận rằng tác động của biến độc lập lên biến phụ thuộc là có ý nghĩa thống kê.
5.5. Khoảng tin cậy của hệ số ước lượng
Khoảng tin cậy của hệ số ước lượng cho biết khoảng giá trị mà hệ số ước lượng có thể nằm trong đó với một mức tin cậy nhất định. Thông thường, khoảng tin cậy 95% được sử dụng để ước lượng giá trị của hệ số. Nếu khoảng tin cậy không bao gồm giá trị 0, bạn có thể kết luận rằng hệ số ước lượng là ý nghĩa thống kê.
5.6. Residuals
Phần residuals cho người dùng biết về các sai số ngẫu nhiên còn lại sau khi đã xây dựng mô hình hồi quy. Nếu sai số ngẫu nhiên phân bố đều và không có liên quan với biến độc lập, thì mô hình hồi quy sẽ có hiệu quả cao.
Trên đây là toàn bộ những chia sẻ của Tri Thức Cộng Đồng về cách chạy mô hình hồi quy trong SPSS đúng chuẩn, hy vọng nó sẽ hữu ích với bạn. Ngoài ra, nếu bạn không có đủ thời gian hoặc kỹ năng để tự chạy mô hình hồi quy tuyến tính trong SPSS, bạn có liên hệ ngay với dịch vụ của chúng tôi. Hiện Tri Thức Cộng Đồng đang cung cấp dịch vụ spss đảm bảo kết quả nhanh chóng và chính xác. Khách hàng quan tâm, vui lòng liên hệ ngay với chúng tôi để được tư vấn cụ thể hơn nhé!
Thông tin liên hệ:
- Hotline: 094 688 3350
- Website: https://trithuccongdong.net/
- Email: ttcd.group@gmail.com
- Địa chỉ:
144 Xuân Thủy, Dịch Vọng Hậu, Cầu Giấy, Hà Nội
2 Võ Oanh, Phường 25, Bình Thạnh, Hồ Chí Minh
9 Đại lộ Temasek, Suntec Tower, Singapore

 14 Tháng 1, 2026
14 Tháng 1, 2026 Share
Share