Descriptive Statistics (thống kê mô tả) là một phương pháp thống kê quen thuộc với những ai đang học và làm việc trong lĩnh vực phân tích hay nghiên cứu khoa học về định lượng. Vậy Descriptive Statistics là gì? thống kê mô tả bằng SPSS, EVIEWS, STATA là như thế nào. Hãy cùng Tri Thức Cộng Đồng tìm hiểu qua bài viết dưới đây.
1. Descriptive statistics là gì?
Descriptive Statistics (thống kê mô tả) là một phương pháp thống kê được sử dụng để tóm tắt, sắp xếp, đơn giản hóa, mô tả và trình bày dữ liệu đã thu thập dưới dạng số hoặc biểu đồ trực quan.

Descriptive statistics là gì?
Trong nghiên cứu về định lượng, sau khi thu thập được các dữ liệu:
- Bước đầu tiên của phân tích thống kê là mô tả đặc điểm của các câu trả lời. Ví dụ như mô tả giá trị trung bình hoặc mối quan hệ giữa các biến dữ liệu.
- Bước tiếp theo sẽ sử dụng thống kê suy luận, nó giúp quyết định xem dữ liệu của bạn có được xác nhận hay không, hoặc sẽ bác bỏ giả thuyết của bạn.
2. Tổng hợp 3 loại thống kê mô tả chính
Thống kê mô tả bao gồm 3 loại chính là các thông số đo lường xu hướng tập trung, đo lường xu hướng biến động và phân phối tần suất, cụ thể như sau:
2.1. Thông số đo lường xu hướng tập trung
- Xu hướng tập trung là mô tả tóm tắt tập dữ liệu bằng cách sử dụng một giá trị duy nhất để phản ánh điểm chính của phân phối dữ liệu.
- Các thông số đo lường xu hướng tập trung dùng để mô tả vị trí trung tâm của phân phối tập dữ liệu, bao gồm: Giá trị trung bình, trung vị và yếu vị.
Đặc điểm

Thông số đo lường xu hướng tập trung
Giá trị trung bình (Mean):
– Giá trị trung bình được tính đơn giản bằng cách lấy tổng các giá trị dữ liệu chia cho kích thước mẫu.
– Công thức: Mean = (x1 + x2 + …xn) / n
– 3 lưu ý về giá trị trung bình cộng:
- Trung bình cộng thường bị ảnh hưởng bởi các giá trị ngoại lệ và các phân phối bất đối xứng.
- Đối với dữ liệu định danh thì không áp dụng trung bình cộng.
- Trung bình cộng hạn chế sử dụng đối với dữ liệu định lượng theo thang đo khoảng.
Trung vị (Median):
– Trung vị là giá trị ở giữa trong một phân bố dữ liệu, nhờ trung vị mà dữ liệu được chia làm hai phần với số liệu bằng nhau ở mỗi bên.
– Nếu m là trung vị của một phân bố dữ liệu thì một nửa giá trị dữ liệu trong phân bố s nhỏ hơn m, số còn lại có giá trị lớn hơn m.
– Trung vị được tính như sau:
- Dữ liệu phải được sắp xếp theo thứ tự tăng dần hoặc giảm dần.
- Nếu số phần tử là số lẻ thì trung vị chính là giá trị nằm ở vị trí giữa.
- Nếu số phần tử là số chẵn thì trung vị là trung bình cộng của 2 giá trị ở giữa.
Yếu vị (Mode): Là con số có tần số xuất hiện nhiều nhất trong mẫu, nếu trong mẫu không có số nào xuất hiện lập lại thì không có mode.
Ví dụ đo lường xu hướng tập trung
Đo lường xu hướng tập trung của một tập hợp thời gian (giây “s”) trong 6 lần chạy cự li 100m của một vận động viên.
A= {10, 9, 11, 10.5, 11, 9.4}
Lời giải
Đầu tiên, sắp xếp số liệu theo thứ tự tăng dần: A= {9 , 9.4, 10, 10.5, 11, 11}
– Giá trị trung bình: Mean = (10 + 9 + 11 + 10.5 + 11 + 9.4) / 6 = 10.15
– Trung vị: Do tập hợp có 6 phần tử là số chẵn nên trung vị là giá trị trung bình cộng của vị trí thứ 3 và thứ 4.
Median = (10 + 10.5) / 2 = 10.25
– Yếu vị: Mode = 11 (xuất hiện 2 lần)
>> Đọc thêm: Hệ Số cronbach alpha SPSS: Định Nghĩa, Các Bước, Lỗi Thường Gặp
2.2. Thông số đo lường xu hướng biến động
- Xu hướng biến động là một thống kê mô tả, tóm tắt phản ánh mức độ phân tán trong một tập hợp dữ liệu.
- Các thông số đo lường xu hướng biến động xác định khoảng cách các điểm dữ liệu rời ra khỏi trung tâm, bao gồm: Khoảng biến thiên, bách phân vị, tứ phân vị, khoảng trải giữa, phương sai và độ lệch chuẩn.
Đặc điểm

Thông số đo lường xu hướng biến động
(1) Khoảng biến thiên (Range):
- Khoảng biến thiên (ký hiệu: R) là đại lượng đo mức trải dài của một tập hợp dữ liệu từ nhỏ nhất đến lớn nhất, được tính bằng cách lấy giá trị lớn nhất trừ cho giá trị nhỏ nhất.
- Công thức: R = Xmax – Xmin
(2) Bách phân vị (Percentile):
– Bách phân vị là đại lượng dùng để ước tính tỷ lệ dữ liệu trong một tập hợp số liệu rơi vào vùng cao hơn hoặc thấp hơn so với một giá trị cho trước.
– 02 kết luận của bách phân vị: Nếu ta có phân vị thứ p∈[0;100] và giá trị vp tại vị trí p thì
- Có ít nhất p% các quan sát có giá trị ≤vp
- Có ít nhất (100 – p)% các quan sát có giá trị ≥vp
– Cách tính bách phân vị:
- Bước 1: Chúng ta sắp xếp dữ liệu theo thứ tự từ bé đến lớn.
- Bước 2: Tính chỉ số i
Chú thích:
+ i: Là vị trí của giá trị dữ liệu tại phân vị thứ p
+ p: Là phân vị thứ p
+ n: Là tổng số quan sát
- Bước 3: Xác định giá trị vp
+ Nếu i là số nguyên: Thì bách phân vị thứ p có giá trị dữ liệu ở vị trí thứ i trong tập hợp dữ liệu.
+ Nếu i là số lẻ: Chúng ta sẽ làm tròn i lên và xuống với số nguyên gần nhất, sau đó tính trung bình hai giá trị dữ liệu ở hai vị trí này trong tập hợp dữ liệu thì ta có được bách phân vị.
(3) Tứ phân vị (Quartile):
- Tứ phân vị là giá trị bằng con số phân chia một nhóm dữ liệu kết quả quan sát thành bốn phần bằng nhau (25% kết quả quan sát). Tứ phân vị là một thành phần của bách phân vị.
- Tứ phân vị có 3 giá trị là phân vị thứ nhất (Q1), thứ 2 (Q2) và thứ 3 (Q3). Ba giá trị phân vị này sẽ chia một tập hợp dữ liệu (sắp xếp theo thứ tự từ bé đến lớn) thành bốn phần có số lượng quan sát đều nhau.
(4) Khoảng trải giữa (InterQuartile Range):
- Khoảng trải giữa (ký hiệu: IQR) còn được gọi khoảng tứ phân vị của dữ liệu. Độ trải giữa cho biết mức độ lan truyền của tập hợp nữa giữa hoặc 50% nữa giữa của dữ liệu.
- Công thức: IQR = Q3 – Q1
- Khoảng trải giữa có thể giúp xác định các giá trị ngoại lệ, một giá trị được cho là ngoại lệ nếu nó nhỏ hơn 1,5*IQR tức là dưới phần tư đầu tiên (Q1 – 1,5*IQR) hoặc nó lớn hơn 1,5*IQR tương đương nằm trên phần tư thứ ba (Q3 + 1,5*IQR).
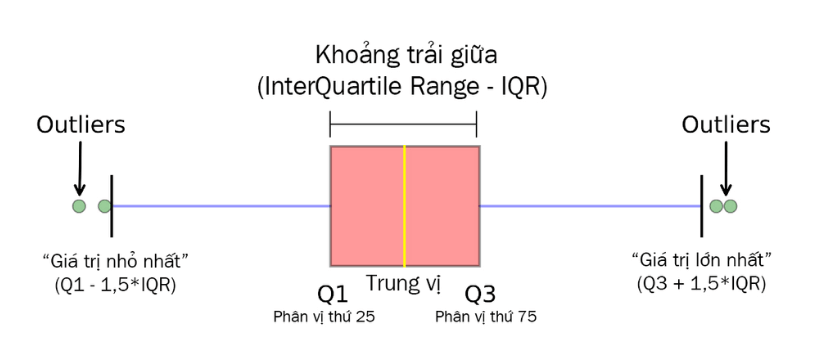
Cách xác định giá trị ngoại lệ bằng khoảng trải giữa
(5) Phương sai (Variance)
- Phương sai là một thước đo thể hiện mức chênh lệch giữa các số liệu trong một tập hợp dữ liệu. Nói cách khác, phương sai là thước đo độ biến thiên của các giá trị xung quanh giá trị trung bình của chúng, cho biết giá trị đó cách giá trị kỳ vọng bao xa.
Công thức:

Bảng công thức của phương sai
02 lưu ý về phương sai:
- Dữ liệu càng trải rộng thì phương sai so với giá trị trung bình càng lớn. Phương sai lớn cho chúng ta biết rằng có nhiều sự biến động trong các giá trị của tập hợp dữ liệu.
- Nếu các quan sát đứng gần nhau thì phương sai sẽ nhỏ.
(6) Độ lệch chuẩn (Standard deviation):
- Độ lệch chuẩn là thước đo độ phân tán của các giá trị so với giá trị trung bình, nó cho biết trung bình mỗi giá trị sẽ nằm bao xa so với giá trị trung bình của chúng trong một tập hợp dữ liệu.
- Độ lệch chuẩn sẽ bị ảnh hưởng bởi các giá trị ngoại lệ và các số âm.
Công thức: Độ lệch chuẩn là căn bậc 2 của phương sai.

Bảng công thức của độ lệch chuẩn
Ví dụ đo lường xu hướng biến động
Đo lường xu hướng biến động bao gồm: Khoảng biến thiên, bách phân vị thứ 72, tứ phân vị, khoảng trải giữa, phương sai và độ lệch chuẩn của một tập hợp thời gian (giây “s”) chạy cự li 100m của một nhóm 7 vận động viên.
B= {10, 9, 11, 10.5, 9.4, 12, 11.5}
Lời giải
Đầu tiên, chúng ta sắp xếp dữ liệu theo thứ tự tăng dần B = {9, 9.4, 10, 10.5, 11, 11.5, 12}.
– Khoảng biến thiên: R = max – min = 12 – 9 = 3
– Bách phân vị thứ 72: i72 = (p*(n+1)) / 100 = (72*(7+1)) / 100 = 5.76
- Vì i72 bằng 5.76 là số lẻ nên chúng ta làm tròn xuống 5 và làm tròn lên 6. Vị trí thứ 5 có giá trị thời gian bằng 11 và ở vị trí thứ 6 là 11.5.
- Tính trung bình cộng 11 và 11.5 là 11.25 => bách phân vị thứ 72 là 11.25.
- Kết luận: Có ít nhất 72% giá trị quan sát nhỏ hơn hoặc bằng 11.25, và ngược lại có ít nhất 28% giá trị quan sát lớn hơn hoặc bằng 11.25.
– Tứ phân vị:
- Tập hợp có 7 quan sát, vậy giá trị trung vị nằm ở vị trí thứ 4 có giá trị là 10.5 => Q2 = 10.5
- Q1 là giá trị nửa dưới dữ liệu, tương ứng B1 = {9, 9.4, 10}. Tập B1 có 3 giá trị, do đó trung vị là 9.4 => Q1 = 9.4
- Q3 là giá trị nửa trên dữ liệu,bao gồm B2 = {11, 11.5, 12}. Tập B2 có 3 giá trị, do đó trung vị là 11.5 => Q3 = 11.5
– Khoảng trải giữa: IQR = Q3 – Q1 = 11.5 – 9.4 = 2.1
– Phương sai:
- Giá trị trung bình của B = (10 + 9 + 11 + 10.5 + 9.4 + 12 + 11.5) / 7 = 10.49
- Phương sai s2 = (1 / 7 – 1)*((10 – 10.49)2 + (9 – 10.49)2 + (11 – 10.49)2 + (10.5 – 10.49)2 + (9.4 – 10.49)2 + (12 – 10.49)2 + (11.5 – 10.49)2) = 1.20145
– Độ lệch chuẩn: s = căn bậc 2 của phương sai = 1.096
2.3. Phân phối tần suất (Frequency Distribution)
- Phân phối tần suất là sự biểu diễn tần suất hoặc số lượng các quan sát ở dạng đồ thị hoặc dạng bảng trong một khoảng nhất định trong thống kê mô tả.
- Mỗi mục dữ liệu được nhập trong bảng hoặc biểu đồ sẽ đi kèm với số lượng hoặc tần suất xuất hiện của các giá trị trong một khoảng, phạm vi hoặc nhóm cụ thể.
- Phân bố tần suất thường được sử dụng trong biểu đồ thanh, biểu đồ tròn và biểu đồ đường.

Phân phối tần suất
– Ví dụ phân phối tần suất
Ví dụ: Xây dựng bảng phân phối đơn giản và theo nhóm của một khảo sát về chiều cao (m) của 15 bạn nam lớp 12C1 trường A.
A = {1.69, 1.72, 1.75, 1.8, 1.65, 1.71, 1.7, 1.6, 1.75, 1.65, 1.7, 1.75, 1.81, 1.81, 1.74}
- Sắp xếp theo thứ tự tăng dần: {1.6, 1.65,1.65, 1.69, 1.7, 1.7, 1.71, 1.72, 1.74, 1.75, 1.75, 1.75, 1.8, 1.81, 1.81 }
- Bảng phân phối tần suất đơn giản
| Chiều cao | Tần số | Tần suất |
| 1.6 | 1 | 6.67% |
| 1.65 | 2 | 13.33% |
| 1.69 | 1 | 6.67% |
| 1.7 | 2 | 13.33% |
| 1.71 | 1 | 6.67% |
| 1.72 | 1 | 6.67% |
| 1.74 | 1 | 6.67% |
| 1.75 | 3 | 20% |
| 1.8 | 1 | 6.67% |
| 1.81 | 2 | 13.33% |
| Tổng | 15 | 100% |
Bảng phân phối tần suất nhóm
| Chiều cao | Tần số | Tần suất |
| 1.6 – 1.7 | 6 | 40% |
| 1.7 – 1.8 | 7 | 46.67% |
| Trên 1.8 | 2 | 13.33% |
| Tổng | 15 | 100% |
Xử lý dữ liệu SPSS là công việc đòi hỏi người sử dụng phải có kỹ năng chuyên môn và dành nhiều thời gian. Deadline đang đến gần, bạn muốn hoàn thiện bài luận văn, báo cao của mình nhưng gặp các trở ngại về thời gian hoặc bạn không biết sử dụng SPSS. Hãy liên hệ ngay dịch vụ hỗ trợ spss của Tri Thức Cộng Đồng để chúng tôi có thể giúp bạn hoàn thành deadline một cách tốt nhất.
3. Vai trò của phương pháp thống kê mô tả
Thông qua thống kê mô tả, chúng ta có thể tóm tắt dữ liệu và mô tả chúng một cách trực quan nhất. Do đó, thống kê mô tả có 5 vai trò chính như sau:

Vai trò của phương pháp thống kê mô tả
- Hiểu rõ tính chất dữ liệu: Thống kê mô tả giúp người đọc hiểu được tính chất của dữ liệu thông qua việc mô tả và sử dụng các biến.
- Biết được ý nghĩa dữ liệu: Biểu diễn kết quả dữ liệu dưới dạng biểu đồ hay số, sẽ giúp người đọc hình dung rõ nhất về ý nghĩa của các dữ liệu mình cần phân tích.
- Trực quan hóa dữ liệu: Nhờ thống kê mô tả người đọc có thể thấy được sự trực quan và sinh động của tập hợp dữ liệu. Do đó, tiếp cận dữ liệu theo cách này sẽ dễ dàng hơn so với dữ liệu thô.
- Đơn giản hóa dữ liệu: Thống kê mô tả biến những thông tin phức tạp của một dữ liệu lớn thành những thông tin ngắn gọn, đơn giản.
- Đánh giá và phân loại dữ liệu: Dựa trên thống kê mô tả chúng ta sẽ đưa ra được những đánh giá, dự đoán hoặc phân loại chính xác về một đối tượng đang quan sát.
4. Phân tích thống kê mô tả bằng SPSS, EVIEWS, STATA
Thống kê mô tả thường được xử lý bởi các phần mềm chuyên dụng như: SPSS, EVIEWS VÀ STATA, chúng là những phần mềm thống kê và phân tích số liệu thiết yếu đối với các nhà phân tích.
SPSS
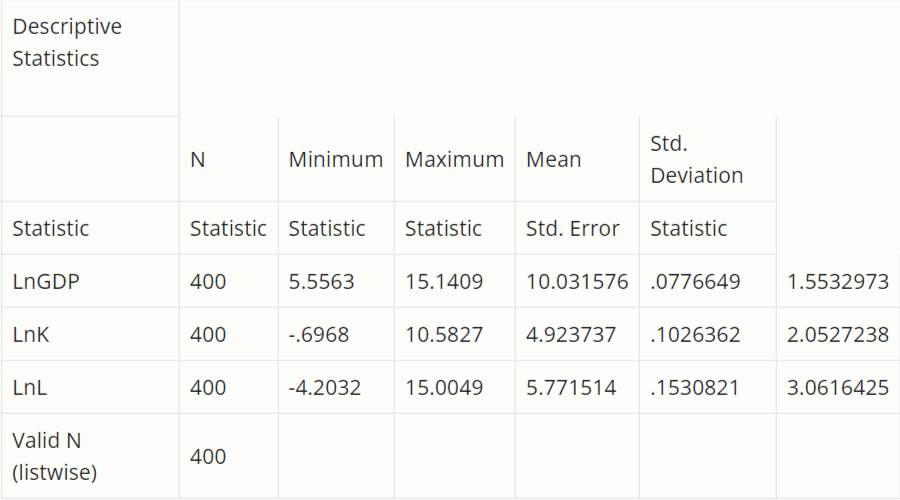
Kết quả thống kê mô tả bằng SPSS
- SPSS là phần mềm phân tích thống kê được nhiều người ưa thích vì dễ sử dụng với giao diện cho phép menu thả xuống để lựa chọn lệnh.
- Khi thực hiện thống kê mô tả chỉ cần chọn lệnh và các biến là có ngay kết quả trên màn hình, đặc biệt là dễ dàng tạo ra các đồ thị chất lượng cao.
- Điểm mạnh của SPSS trong thống kê mô tả là đại lượng phương sai.
EVIEWS
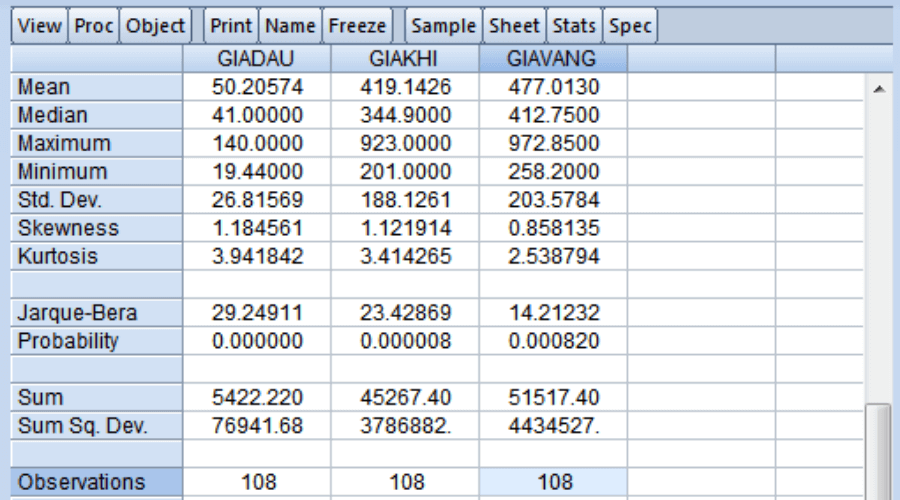
Kết quả thống kê mô tả bằng EVIEWS
- EVIEWS (Econometric Views) là phần mềm được sử dụng trong thống kê và kinh tế lượng, phục vụ việc phân tích và dự báo dữ liệu.
- EVIEWS có khả năng linh hoạt trong thao tác, quản lý dữ liệu dễ dàng, kết quả hiển thị nhanh và dễ dàng hiểu được. Do đó, nó đang dần trở nên phổ biến được nhiều người sử dụng.
- Trong thống kê mô tả, EVIEWS giúp phân tích sự tác động của các yếu tố kinh tế vĩ mô lên biến cần nghiên cứu với đề tài kinh tế.
STATA
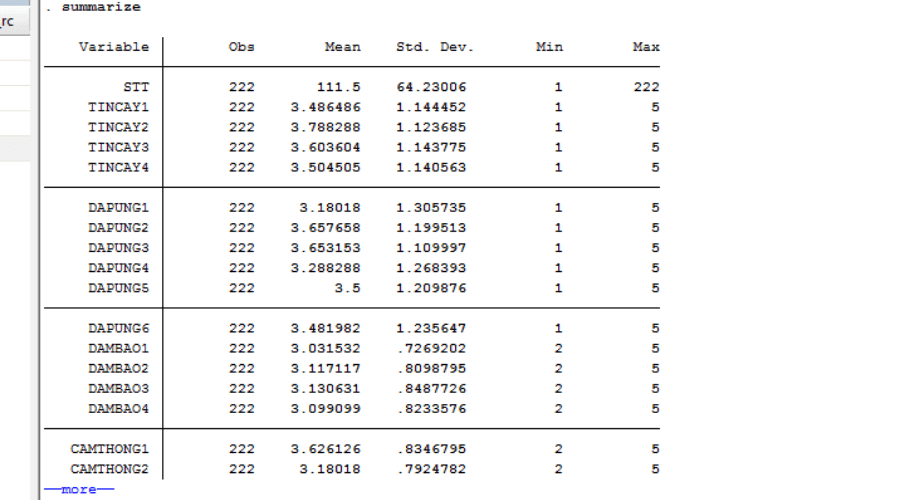
Kết quả thống kê mô tả bằng STATA
- STATA là một phần mềm thống kê phù hợp với người mới bắt đầu vì dễ học và có nhiều chức năng, được sử dụng phổ biến trong lĩnh vực kinh tế, xã hội học, khoa học chính trị,..
- Trong thống kê mô tả, STATA yếu về phân tích phương sai, phân tích nhóm.
5. Phân biệt thống kê mô tả và thống kê suy luận (Inferential statistics)

Phân biệt thống kê mô tả và thống kê suy luận
Thống kê là phương pháp thu thập, phân tích và biểu diễn dữ liệu. Thống kê phổ biến trong lĩnh vực nghiên cứu và được chia thành 02 loại khác biệt bao gồm thống kê mô tả và thống kê suy luận (suy diễn). Cụ thể chúng có 5 điểm khác biệt như sau:
| Yếu tố
so sánh |
Thống kê mô tả
(Descriptive Statistics) |
Thống kê suy luận
(Inferential statistics) |
| Định nghĩa | Là một nhánh thống kê liên quan đến việc mô tả thuộc tính chính của dữ liệu định lượng (dân số) đang quan sát. | Là nhánh của thống kê, đưa ra kết luận về dân số liên quan đến tập dữ liệu trên cơ sở quan sát và phân tích mẫu. |
| Chức năng | Phản ánh tổng quát đối tượng đang nghiên cứu. | Đi đến kết luận để tìm hiểu về dân số, vượt ra ngoài những dữ liệu có sẵn. |
| Phương pháp
thực hiện |
– Thu thập số liệu
– Giải thích dữ liệu – Tóm tắt mẫu – Tính toán dữ liệu – Trình bày và mô tả các đặc trưng khác nhau. |
– Ước lượng các đặc trưng của tổng thể.
– Phân tích các mối liên hệ giữa những hiện tượng nghiên cứu. – Dự đoán hoặc đưa ra quyết định trên cơ sở thu thập thông tin từ kết quả quan sát mẫu. |
| Ứng dụng | Mô tả một tình huống | Giải thích các cơ hội xảy ra của một sự kiện, hiện tượng |
| Mẫu kết quả cuối cùng | Biểu đồ, đồ thị và bảng | Xác suất |
Bảng so sánh thống kê mô tả và thống kê suy luận
6. Câu hỏi thường gặp
Tri Thức Cộng Đồng giới thiệu đến bạn đọc 03 câu hỏi thường gặp liên quan đến thống kê mô tả, cụ thể bao gồm:

Câu hỏi thường gặp trong thống kê mô tả
Câu 1: Kể tên ba loại thống kê mô tả chính?
Trả lời: Ba loại thống kê mô tả chính gồm: Phân phối tần suất, các thước đo xu hướng trung tâm và các thước đo xu hướng biến động.
Câu 2: Sự khác biệt giữa thống kê mô tả và thống kê suy luận là gì?
Trả lời: Thống kê mô tả tóm tắt các đặc điểm của dữ liệu, thống kê suy luận dùng để kiểm tra giả thuyết hoặc đánh giá dữ liệu.
Câu 3: Sự khác biệt giữa thống kê mô tả đơn biến, lưỡng biến và đa biến là gì?
Trả lời: Thống kê mô tả đơn biến chỉ tóm tắt một biến, lưỡng biến là so sánh hai biến và đa biến là so sánh nhiều hơn hai biến dữ liệu.
Bài viết nhằm cung cấp thông tin đến bạn đọc với chủ đề Descriptive Statistics là gì? cũng như giới thiệu cách xử lý thống kê mô tả bằng SPSS, EVIEWS, STATA. Qua đây, chúng tôi mong rằng bạn đọc đã có thêm nhiều kiến thức bổ ích và có được kết quả tốt nhất trong việc áp dụng thống kê mô tả cho bài nghiên cứu của mình. Chúc các bạn thành công!

 14 Tháng 1, 2026
14 Tháng 1, 2026 Share
Share